- Bernoulliの不等式
- 数列(sequences)
- Cauchyの平均値の定理
- 不定形の極限値(limit of indeterminate forms)
- D'Alembertの判定法
- 正項級数(nonnegative term series)
- Euler e
- no title
- Gamma関数
- 定積分の定義の拡張(extension of definite integrals)
- Gaussの発散定理
- ベクトル積分定理(integral theorems of vector
- Greenの定理
- ベクトル積分定理(integral theorems of vector
- L'Hospitalの定理
- 不定形の極限値(limit of indeterminate forms)
- Lagrangeの乗数法
- 条件付極値(extremum with side conditions)
- Landauのスモールオー
- Taylorの定理(Taylor's theorem)
- Landauのビッグオー
- Taylorの定理(Taylor's theorem)
- Leibnizの定理
- 高次導関数(higher-order derivatives)
| 交項級数(alternating series)
- Maclaurin展開
- Taylorの定理(Taylor's theorem)
- Riemann和
- 定積分(definite integral)
- Rolleの定理
- 平均値の定理と関数の性質(mean-value theorem and properties
- Stokesの定理
- ベクトル積分定理(integral theorems of vector
- Taylor展開
- Taylorの定理(Taylor's theorem)
- Taylorの定理
- Taylorの定理(Taylor's theorem)
- telescoping sum
- 級数の定義(definition of series)
- Wallis
- 定積分の計算(calculation of integrals)
- Weierstrassの判定法
- *関数項級数(series of functions)
- アルキメデスの渦線
- 曲線の概形(curve sketching)
- 一意性
- オイラー e(Euler e)と超越関数
- 1対1の関数
- 関数の定義(definition of function)
- 一様収束する
- *関数項級数(series of functions)
- 1価関数
- 関数の定義(definition of function)
- 一般項
- 数列(sequences)
- 一般調和級数
- 級数の定義(definition of series)
- 陰関数
- 陰関数(implicit functions)
- 陰関数の存在定理
- 陰関数(implicit functions)
- 上に凸
- 平均値の定理と関数の性質(mean-value theorem and properties
- 上に有界
- 数列(sequences)
| *実数の連続性(continium)
- 内面積
- 2重積分(double integrals)
- n回微分可能
- 高次導関数(higher-order derivatives)
 乗根
乗根
- 数(NUMBERS)
- 閉集合
- 関数の極限(limit of function)
| 関数の極限(limit of function)
- 回転
- 関数の極限(limit of function)
| ベクトル場の発散(divergence of vector field)
- 下界
- *実数の連続性(continium)
- 下限
- *実数の連続性(continium)
- 加速度ベクトル
- 点の運動(motion of objects)
- 割線
- 導関数(derivatives)
- 関数項級数
- *関数項級数(series of functions)
- 奇関数
- 関数の定義(definition of function)
| 定積分の計算(calculation of integrals)
- 逆関数
- 関数の定義(definition of function)
- 逆関数定理
- 関数の定義(definition of function)
- 逆関数の微分法
- 微分法(Differentiation Formulas)
- 逆三角関数
- 初等関数(elementary functions)
- 逆正弦関数
- 初等関数(elementary functions)
- 逆正椄関数
- 初等関数(elementary functions)
- 逆余弦関数
- 初等関数(elementary functions)
- 級数
- 級数の定義(definition of series)
- 境界
- 関数の極限(limit of function)
- 境界点
- 関数の極限(limit of function)
- 狭義の単調減少関数
- 関数の定義(definition of function)
- 狭義の単調増加関数
- 関数の定義(definition of function)
- 極
- 曲線の概形(curve sketching)
- 極限
- 数列(sequences)
- 極限値
- 関数の極限(limit of function)
| 数列(sequences)
- 極座標
- 曲線の概形(curve sketching)
- 極座標系
- 曲線の概形(curve sketching)
- 極軸
- 曲線の概形(curve sketching)
- 極小
- 平均値の定理と関数の性質(mean-value theorem and properties
- 極小値
- 2変数関数の極値(extreme values)
- 曲線の長さ
- 定積分の応用(applications of definite integral)
- 極大
- 平均値の定理と関数の性質(mean-value theorem and properties
- 極大値
- 2変数関数の極値(extreme values)
- 極値
- 平均値の定理と関数の性質(mean-value theorem and properties
| 2変数関数の極値(extreme values)
- 極方程式
- 曲線の概形(curve sketching)
- 曲率
- 曲線(space curves)
- 逆正弦関数の主値
- 初等関数(elementary functions)
- 逆正椄関数の主値
- 初等関数(elementary functions)
- 逆余弦関数の主値
- 初等関数(elementary functions)
- 偶関数
- 関数の定義(definition of function)
| 定積分の計算(calculation of integrals)
- 区間Iで微分可能
- 導関数(derivatives)
- 区分求積法
- 定積分(definite integral)
- 区分的に滑らかな曲線
- 線積分(line integrals)
- グラフ
- 関数の定義(definition of function)
| 関数の定義(definition of functions)
- 原始関数
- 不定積分(indefinite integrals)
- 懸垂線
- オイラー e(Euler e)と超越関数
- 項
- 数列(sequences)
- 広義積分
- 定積分の定義の拡張(extension of definite integrals)
- 広義の定積分
- 定積分の定義の拡張(extension of definite integrals)
- 交項級数
- 交項級数(alternating series)
- 合成関数
- 関数の定義(definition of function)
| 関数の定義(definition of function)
- 合成関数の微分法
- 微分法(Differentiation Formulas)
- 合成法則
- 関数の定義(definition of function)
- 勾配
- 全微分(total differential)
- 項別微分の定理
- *関数項級数(series of functions)
- 項別積分の定理
- *関数項級数(series of functions)
- 弧長
- 曲線(space curves)
- 弧度法
- 初等関数(elementary functions)
- 弧の長さ
- 定積分の応用(applications of definite integral)
- 最小な上界
- *実数の連続性(continium)
- 最大・最小値の定理
- 連続関数(continuous functions)
| 連続関数(continuous functions)
- 最大な下界
- *実数の連続性(continium)
- 三角関数
- 初等関数(elementary functions)
- 三角不等式
- 絶対値の不等式
- 指数
- 累乗
- 指数関数
- オイラー e(Euler e)と超越関数
- 自然数
- 数(NUMBERS)
- 下に凸
- 平均値の定理と関数の性質(mean-value theorem and properties
- 下に有界
- 数列(sequences)
| *実数の連続性(continium)
- 質量
- 3重積分(triple integrals)
- 質点系の重心
- 3重積分(triple integrals)
- ジャコビアン
- 変数変換(change of variables)
- 重積分公式
- 2重積分(double integrals)
- 収束する
- 数列(sequences)
| 級数の定義(definition of series)
- 収束半径
- *関数項級数(series of functions)
- 従法線単位ベクトル
- 点の運動(motion of objects)
- 縦線集合
- 累次積分(repeated integrals)
- 主法線単位ベクトル
- 曲線(space curves)
- 条件収束
- 定積分の定義の拡張(extension of definite integrals)
- 上界
- *実数の連続性(continium)
- 上限
- *実数の連続性(continium)
- 条件収束
- 交項級数(alternating series)
- 初等関数
- 初等関数(elementary functions)
- 初速度
- 高次導関数(higher-order derivatives)
- 真性不連続点
- 連続関数(continuous functions)
- 心臓形
- 曲線の概形(curve sketching)
- 数直線
- *実数の連続性(continium)
- 数列
- 数列(sequences)
- 数列の基礎定理
- オイラー e(Euler e)と超越関数
| *実数の連続性(continium)
- スカラー場
- スカラー場とベクトル場(scalar field and vector
- スカラーポテンシャル
- スカラー場とベクトル場(scalar field and vector
- 整関数
- 初等関数(elementary functions)
- 整級数
- *関数項級数(series of functions)
- 整級数の基本性質
- *関数項級数(series of functions)
- 正項級数
- 正項級数(nonnegative term series)
- 整式
- 初等関数(elementary functions)
- 整数
- 数(NUMBERS)
- 積分可能
- 定積分(definite integral)
| 広義積分(improper integrals)
- 積分定数
- 不定積分(indefinite integrals)
- 積分する
- 不定積分(indefinite integrals)
- 積分順序の交換
- 累次積分(repeated integrals)
- 積分判定法
- 正項級数(nonnegative term series)
- 接線
- 導関数(derivatives)
- 接線単位ベクトル
- 曲線(space curves)
- 接線ベクトル
- 曲線(space curves)
- 絶対収束
- 定積分の定義の拡張(extension of definite integrals)
| 交項級数(alternating series)
- 絶対値
- 数(NUMBERS)
- 接平面
- 全微分(total differential)
| 曲面(surface)
- 線積分
- 線積分(line integrals)
- 尖点
- 曲線の概形(curve sketching)
- 全微分
- 全微分(total differential)
- —可能
- 全微分(total differential)
- 像
- 関数の定義(definition of function)
| 関数の定義(definition of functions)
- 双曲線関数
- オイラー e(Euler e)と超越関数
- 増分
- 導関数(derivatives)
- 束
- 面積分(surface integrals)
- 束積分
- 面積分(surface integrals)
- 速度ベクトル
- 点の運動(motion of objects)
- 外面積
- 2重積分(double integrals)
- 第n次導関数
- 高次導関数(higher-order derivatives)
- 第
 部分和
部分和
- 級数の定義(definition of series)
- 代数学の基本定理
- 有理関数の積分法(integration of rational functions)
- 対数関数
- オイラー e(Euler e)と超越関数
| オイラー e(Euler e)と超越関数
- 対数微分法
- 微分法(Differentiation Formulas)
- 第
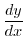 次導関数
次導関数
- 高次導関数(higher-order derivatives)
- 第2次偏導関数
- 偏導関数(partial derivatives)
- 互いに素
- 数(NUMBERS)
- 多価関数
- 関数の定義(definition of function)
- 多重積分
- 2重積分(double integrals)
- ダミー変数
- 不定積分(indefinite integrals)
- 単一閉曲線
- ベクトル積分定理(integral theorems of vector
- 単調減少数列
- 数列(sequences)
- 単調増加数列
- 数列(sequences)
- 値域
- 関数の定義(definition of function)
| 関数の定義(definition of functions)
- 置換積分法
- 置換積分法(integration by substitution)
- 実数
- 数(NUMBERS)
- 中間値の定理
- 連続関数(continuous functions)
| 連続関数(continuous functions)
| *実数の連続性(continium)
- 重力加速度定数
- 高次導関数(higher-order derivatives)
- 循環小数
- 数(NUMBERS)
- 循環小数(recurring decimals)
- 数(NUMBERS)
- 超越関数
- オイラー e(Euler e)と超越関数
- 除去可能な不連続点
- 連続関数(continuous functions)
- 底
- 累乗
- 定義域
- 関数の定義(definition of function)
| 関数の定義(definition of functions)
- 定積分
- 定積分(definite integral)
- Taylorの多項式
- Taylorの定理(Taylor's theorem)
- 等位面
- 関数の定義(definition of functions)
| スカラー場とベクトル場(scalar field and vector
- 導関数
- 導関数(derivatives)
- 等高線
- 関数の定義(definition of functions)
- 内点
- 関数の極限(limit of function)
- 滑らかな曲線
- 曲線(space curves)
- 滑らかな曲面
- 2重積分の応用(application of double integrals)
- 2項定理
- オイラー e(Euler e)と超越関数
- 2重積分可能
- 2重積分(double integrals)
- 2分法
- 連続関数(continuous functions)
- 2変数のTaylorの定理
- 2変数関数の極値(extreme values)
- ねじれ率
- 点の運動(motion of objects)
- 媒介変数
- 微分法(Differentiation Formulas)
- 媒介変数表示による関数の微分法
- 微分法(Differentiation Formulas)
- 背理法
- 数(NUMBERS)
- はさみうちの定理
- 関数の極限(limit of function)
| 数列(sequences)
- 発散
- ベクトル場の発散(divergence of vector field)
- 発散する
- 数列(sequences)
| 級数の定義(definition of series)
- 比較判定法
- 正項級数(nonnegative term series)
- 微分積分学の基本定理
- 定積分(definite integral)
- 左側極限値
- 連続関数(continuous functions)
- 左側微分係数
- 導関数(derivatives)
- 左側連続
- 連続関数(continuous functions)
- 微分
- 導関数(derivatives)
- —可能
- 導関数(derivatives)
- 係数
- 導関数(derivatives)
- —する
- 導関数(derivatives)
- 微分可能
- ベクトル関数(vector functions)
- v 曲線
- 曲面(surface)
- 不定形
- 関数の極限(limit of function)
| 数列(sequences)
| 不定形の極限値(limit of indeterminate forms)
- 不定積分
- 不定積分(indefinite integrals)
- 負の指数
- 累乗
- 部分積分法
- 部分積分法(integration by parts)
- 部分分数分解
- 有理関数の積分法(integration of rational functions)
- 平均値の定理
- 平均値の定理と関数の性質(mean-value theorem and properties
- 閉包
- 関数の極限(limit of function)
- 平方根
- 数(NUMBERS)
- 平面上のGreenの定理
- ベクトル積分定理(integral theorems of vector
- 閉領域
- 関数の極限(limit of function)
- へービサイド展開
- 有理関数の積分法(integration of rational functions)
- ベキ関数
- オイラー e(Euler e)と超越関数
- ベクトル関数
- ベクトル関数(vector functions)
- ベクトル値関数
- ベクトル関数(vector functions)
- ベクトル場
- 全微分(total differential)
| スカラー場とベクトル場(scalar field and vector
- ベルヌーイのラムニスケイト
- 曲線の概形(curve sketching)
- 変曲点
- 平均値の定理と関数の性質(mean-value theorem and properties
- 偏導関数
- 偏導関数(partial derivatives)
- 偏微分
- 偏導関数(partial derivatives)
- —可能
- 偏導関数(partial derivatives)
- 方向微分
- gradientと方向微分(grad and directional derivatives)
- 法線ベクトル
- 曲線(space curves)
| 曲面(surface)
- 保存場
- スカラー場とベクトル場(scalar field and vector
- Maclaurinの定理
- Taylorの定理(Taylor's theorem)
- 右側極限値
- 連続関数(continuous functions)
- 右側微分係数
- 導関数(derivatives)
- 右側連続
- 連続関数(continuous functions)
- 向きづけられる曲面
- ベクトル積分定理(integral theorems of vector
- 無限回微分可能
- 高次導関数(higher-order derivatives)
- 無限積分
- 定積分の定義の拡張(extension of definite integrals)
| 定積分の定義の拡張(extension of definite integrals)
- 無限等比級数
- 級数の定義(definition of series)
- 無理関数
- 初等関数(elementary functions)
| 初等関数(elementary functions)
- 無理数
- 数(NUMBERS)
- 面積確定
- 2重積分(double integrals)
- 面積素
- 曲面(surface)
- 面積分
- 面積分(surface integrals)
- 有界
- 数列(sequences)
| *実数の連続性(continium)
| 関数の極限(limit of function)
- u 曲線
- 曲面(surface)
- 有理関数
- 初等関数(elementary functions)
| 初等関数(elementary functions)
- 有理数
- 数(NUMBERS)
- 横線集合
- 累次積分(repeated integrals)
- Lagrangeの剰余数
- Taylorの定理(Taylor's theorem)
- ラプラシアン
- ベクトル場の発散(divergence of vector field)
- ラプラスの方程式
- ベクトル場の発散(divergence of vector field)
- 力線
- スカラー場とベクトル場(scalar field and vector
- リマソン
- 曲線の概形(curve sketching)
- 流線
- スカラー場とベクトル場(scalar field and vector
- 領域
- 関数の極限(limit of function)
- 累次積分
- 累次積分(repeated integrals)
- 累乗
- 累乗
- 連結
- 関数の極限(limit of function)
- 連続
- 連続関数(continuous functions)
 乗根
乗根
 部分和
部分和
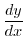 次導関数
次導関数