Next: 陰関数(implicit functions) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 合成関数の偏微分法(differentiation of composite functions) 目次 索引
1変数の極値については3章で学びました.ここでは2変数の極値について考えてみます.
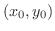 の
の 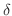 近傍内のすべての点
近傍内のすべての点 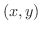 に対して
に対して
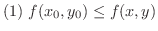 が成り立つとき,関数
が成り立つとき,関数  は点
は点
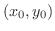 で極小になるといい,
で極小になるといい,
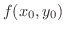 を
を  の 極小値(local minimum) という.
の 極小値(local minimum) という.
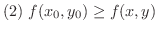 が成り立つとき,関数
が成り立つとき,関数  は点
は点
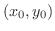 で極大になるといい,
で極大になるといい,
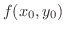 を
を  の 極大値(local maximum) という.また,極小値と極大値を一括して極値(extrema) という.
の 極大値(local maximum) という.また,極小値と極大値を一括して極値(extrema) という.
1変数のとき関数  が
が  で極値をとれば
で極値をとれば
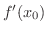 が存在し,かつ
が存在し,かつ
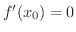 ,または
,または
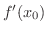 は存在しないのどちらかでした.2変数でも同じようなことがいえるか考えてみましょう.
は存在しないのどちらかでした.2変数でも同じようなことがいえるか考えてみましょう.
 が
が
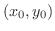 で極値をとれば,次のどちらかが成り立つ.
で極値をとれば,次のどちらかが成り立つ.
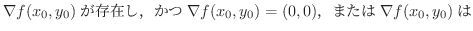 存在しない
存在しない
証明
 だけの関数
だけの関数
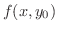 は
は  で極値をとるから,
で極値をとるから,
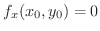 または
または
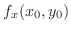 は存在しない. 同様に
は存在しない. 同様に
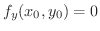 または
または
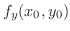 は存在しない.
は存在しない.

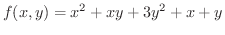
解
 が
が
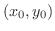 で極値をとるとすれば
で極値をとるとすれば
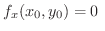 したがって
したがって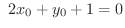
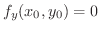 したがって
したがって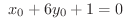
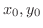 について解くと
について解くと
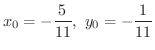
 は点
は点
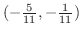 で極値をとる可能性があることが分かりました.しかし,これが極小値なのか極大値なのかさらに調べてみなければなりません.
で極値をとる可能性があることが分かりました.しかし,これが極小値なのか極大値なのかさらに調べてみなければなりません.

そこで,2変数の関数の極値の判定には次の定理があります.
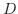 で
で
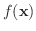 は
は 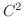 級とする.領域
級とする.領域 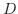 内の点
内の点
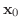 で
で
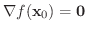 であるとき,
であるとき,
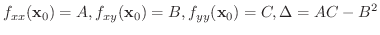
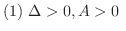 ならば
ならば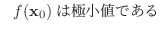
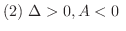 ならば
ならば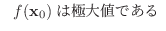
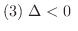 ならば
ならば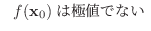
この定理を証明するのに2変数関数のTaylorの定理を用います.
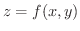 が点
が点
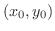 の近傍で
の近傍で  級ならば,この近傍内にある
級ならば,この近傍内にある
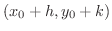 に対して,
に対して,
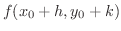 |
 |
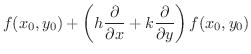 |
|
 |
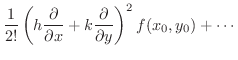 |
||
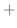 |
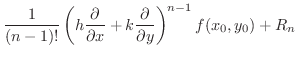 |
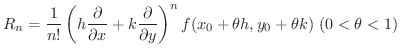
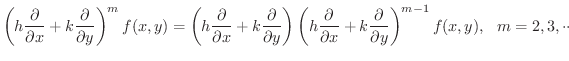
Taylorの定理で
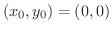 のとき,マクローリンの定理といいます.
のとき,マクローリンの定理といいます.
証明
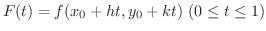 とおくと,
とおくと, 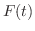 は
は 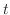 の
の 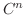 級関数であるから,1変数関数のTaylorの定理より
級関数であるから,1変数関数のTaylorの定理より
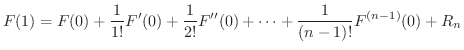
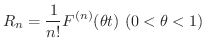
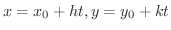 とおくと
とおくと
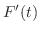 |
 |
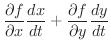 |
|
 |
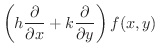 |
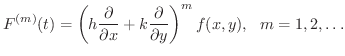
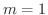 はすでに成り立つので,
はすでに成り立つので, 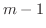 まで成り立つと仮定すると
まで成り立つと仮定すると
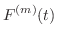 |
 |
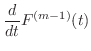 |
|
 |
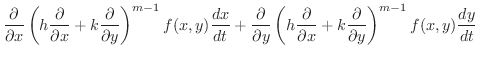 |
||
 |
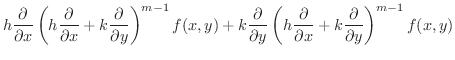 |
||
 |
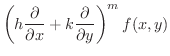 |

やっと2変数の極値に関する定理の証明ができます.
証明
Taylorの定理より,
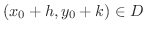 に対して
に対して
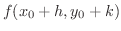 |
 |
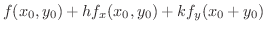 |
|
 |
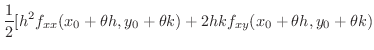 |
||
 |
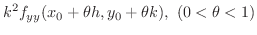 |
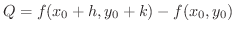 とおくと,
とおくと,
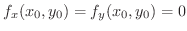 より
より
![$\displaystyle Q = \frac{1}{2}[h^2 f_{xx}(x_{0}+\theta h,y_{0}+\theta k) + 2hkf_...
...(x_{0}+\theta h,y_{0}+\theta k) + k^2 f_{yy} (x_{0}+\theta h,y_{0}+\theta k) ] $](img3639.png)
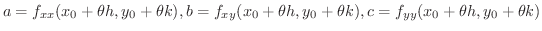 とおくと,
とおくと,
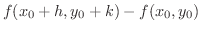 の符号は
の符号は
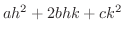 の符号によってきまる.ここで
の符号によってきまる.ここで
![$\displaystyle Q = \frac{1}{2}\left(ah^2 + 2bhk + ck^2\right) = \frac{a}{2}\left[(h + \frac{bk}{a})^2 + \frac{(ac - b^2)k^2}{a^2}\right] $](img3643.png)
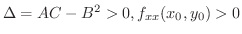 のときは,
のときは,  が
が 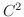 級の関数であるから
級の関数であるから 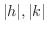 が十分に小さく,しかも同時に0とならないならば,どのような
が十分に小さく,しかも同時に0とならないならば,どのような 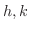 をとっても
をとっても
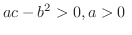 となるので
となるので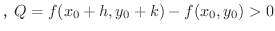
 は極小値となる.
は極小値となる.
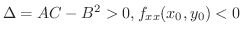 のときは,
のときは,  が
が 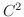 級の関数であるから
級の関数であるから 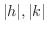 が十分に小さく,しかも同時に0とならないならば,どのような
が十分に小さく,しかも同時に0とならないならば,どのような 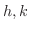 をとっても
をとっても
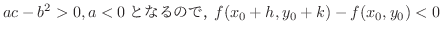
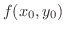 は極大値となる.
は極大値となる.
次に
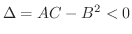 の場合を考える.もし
の場合を考える.もし
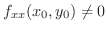 ならば
ならば
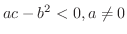 とできるが,
とできるが,
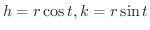 とおくと,
とおくと,
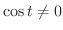 のとき,
のとき,
 |
 |
![$\displaystyle ah^2 + 2bhk + ck^2 = r^{2}[a\cos^{2}{t} + 2b\cos{t}\sin{t} + c \sin^{2}{t}]$](img3657.png) |
|
 |
![$\displaystyle r^{2}\cos^{2}{t}[a + 2b \tan{t} + c \tan^{2}{t}]$](img3658.png) |
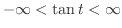 だから,
だから, 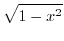 は
は 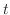 により正にも負にもなる.
により正にも負にもなる.

この定理を使って先ほどの問題を解いてみます,
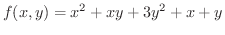
解
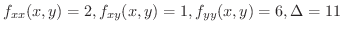
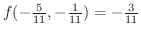 は極小値になります.
は極小値になります.

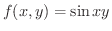 を点
を点
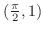 において2次の項までテイラー展開しよう.
において2次の項までテイラー展開しよう.
解
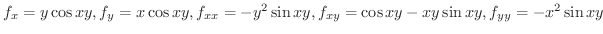 より,定理6.7において,
より,定理6.7において,
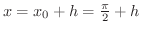 ,
,
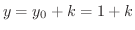 とおくと,
とおくと,
 |
 |
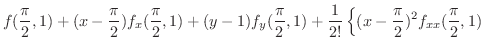 |
|
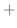 |
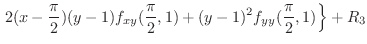 |
||
 |
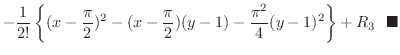 |