Next: 条件付極値(extremum with side conditions) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 2変数関数の極値(extreme values) 目次 索引
方程式
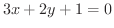 から,
から,  の関数としての
の関数としての  つまり
つまり
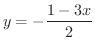 を考えることができます.一般に2変数関数
を考えることができます.一般に2変数関数 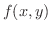 に対して,1変数関数
に対して,1変数関数 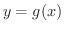 が常に
が常に
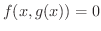 を満たすとき,
を満たすとき, 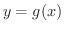 を方程式
を方程式
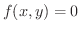 から定まる陰関数(implicit function) といいます.
から定まる陰関数(implicit function) といいます.
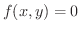 から定まる陰関数
から定まる陰関数 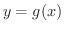 を求めることは,
を求めることは,
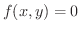 を
を  について解くことと同じです.しかし
について解くことと同じです.しかし  の形によっては,ある
の形によっては,ある  の値に対して,
の値に対して,
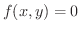 を満たす
を満たす  の値は1つもないことがあります.そこでどんな場合に陰関数が存在するかが問題になります.これについて,次の定理があります.
の値は1つもないことがあります.そこでどんな場合に陰関数が存在するかが問題になります.これについて,次の定理があります.
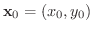 を含む領域
を含む領域  で
で 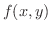 は
は 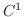 級とする.
級とする.
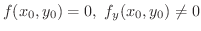
 の近傍で
の近傍で
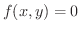 の定める陰関数
の定める陰関数 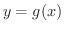 がただ1つ定まり,次の関係が成り立つ.
がただ1つ定まり,次の関係が成り立つ.
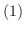 |
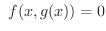 |
||
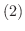 |
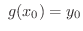 |
||
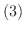 |
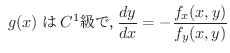 |
つまり,
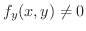 となる点の近くでは(1)を満足する陰関数
となる点の近くでは(1)を満足する陰関数  が存在し.さらに
が存在し.さらに  に関して微分可能であることが証明されています.だから(1)の両辺の全微分をとると
に関して微分可能であることが証明されています.だから(1)の両辺の全微分をとると
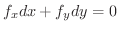
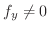 により
により
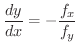
 について微分すると
について微分すると
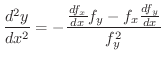
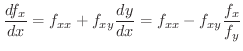
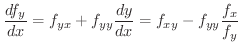
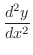 |
 |
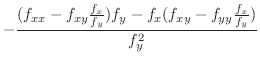 |
|
 |
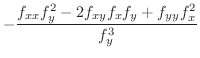 |
となります.
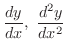 を求めてみましょう.
を求めてみましょう.
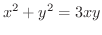
解
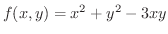 とおき,
とおき, 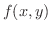 の全微分を求めると,
の全微分を求めると,
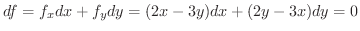
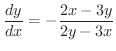
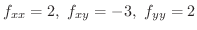 なので,
なので,
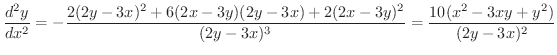

2変数関数のときと同じように3変数関数 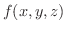 において,
において,
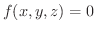
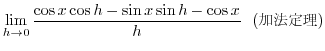 の陰関数
の陰関数
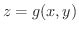 について考えることができます.
について考えることができます.
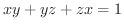 から定まる
から定まる 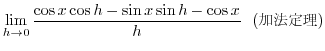 の陰関数
の陰関数
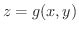 について
について
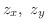 を求めてみましょう.
を求めてみましょう.
解
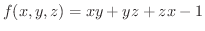 の全微分をとると
の全微分をとると
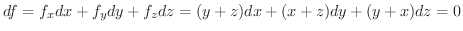
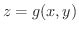 より
より
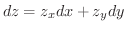
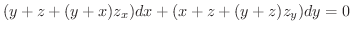
 と
と  は独立変数であることに注意すると,
は独立変数であることに注意すると,
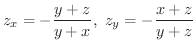

次に2つの式
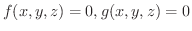 から
から 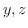 が
が  の陰関数として定まる場合について考えてみましょう.
の陰関数として定まる場合について考えてみましょう.
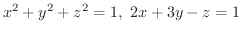 から,
から, 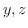 が
が  の関数として定まるとき
の関数として定まるとき
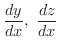 を求めてみましょう.
を求めてみましょう.
解
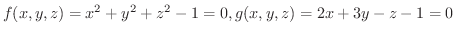 とおき,全微分をとると,
とおき,全微分をとると,
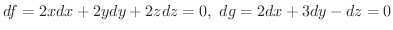
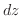 を消去すると
を消去すると
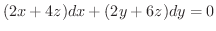
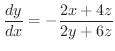
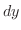 を消去すると
を消去すると
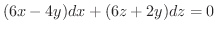
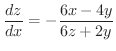

*陰関数の極値
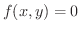 から定まる陰関数
から定まる陰関数 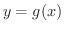 の極値を考えてみましょう.まず
の極値を考えてみましょう.まず  で極値
で極値
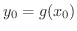 をとるとすると,陰関数の存在定理より
をとるとすると,陰関数の存在定理より
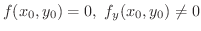
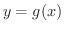 が極値をとるためには
が極値をとるためには
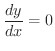 でなければならないので
でなければならないので
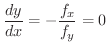
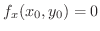 .次に
.次に
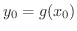 が極小値か極大値か調べるために,
が極小値か極大値か調べるために,
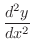 を求めると
を求めると
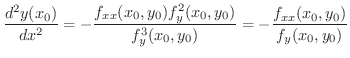
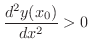
 で極小値
で極小値
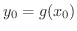 ,
,
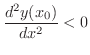
 で極大値
で極大値
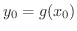 .ここまでをまとめると次の定理を得ます.
.ここまでをまとめると次の定理を得ます.
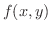 は
は 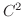 級とする.
級とする.
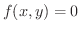 より定まる陰関数
より定まる陰関数 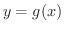 が
が  で極値
で極値
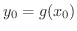 をとるならば,
をとるならば,
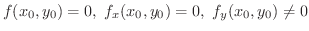
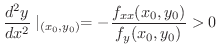 ならば
ならば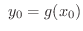 極小値である.
極小値である.
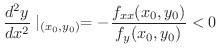 ならば
ならば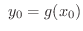 極大値である.
極大値である.
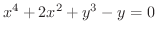 から定まる
から定まる  の関数
の関数 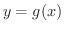 の極値を求めてみましょう.
の極値を求めてみましょう.
解
まず,
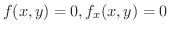 を満たす
を満たす 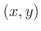 を求めます.
を求めます.
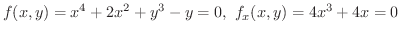
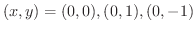 .次に
.次に
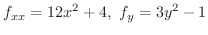
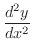 を計算すると
を計算すると
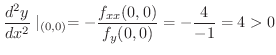
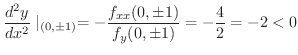
 のときの
のときの 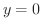 は極小値,
は極小値,  のときの
のときの 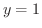 は極大値,
は極大値,  のときの
のときの 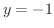 も極大値です.
も極大値です.

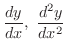 を求めよう.
を求めよう.
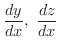 を求めよう.
を求めよう.
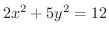 上の点
上の点
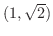 における接線と法線を求めよう.
における接線と法線を求めよう.
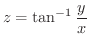 上の点
上の点
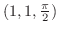 における接平面と法線を求めよう.
における接平面と法線を求めよう.
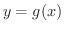 の極値を求めよう.
の極値を求めよう.