Next: 重積分法(MULTIPLE INTEGRATION) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 陰関数(implicit functions) 目次 索引
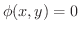 という条件のもとで,
という条件のもとで,  の極値を求める問題を考えてみましょう.
の極値を求める問題を考えてみましょう.
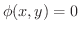 より
より
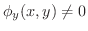 ならば
ならば
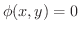 を満たす陰関数
を満たす陰関数 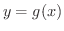 が定まります.いま
が定まります.いま
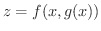 が
が
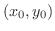 で極値をとるとすると,
で極値をとるとすると,
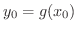 かつ
かつ 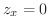 より,
より,
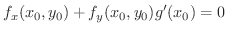
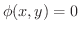 を
を  で微分すると
で微分すると
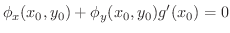
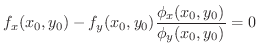
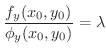
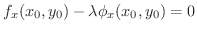
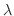 が存在することが分かります.これより次の定理を得ます.
が存在することが分かります.これより次の定理を得ます.
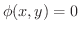 のもとで,
のもとで,  が極値をとる
が極値をとる  の値は,
の値は,
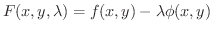
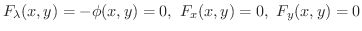
この定理は幾何学的に考えると次のように考えることができます.
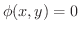 よりベクトル
よりベクトル
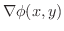 は曲線
は曲線
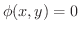 と直交します.また
と直交します.また  が条件
が条件
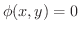 のもとで極値をとるということは,
のもとで極値をとるということは,
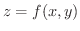 の等高線
の等高線
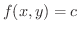 と
と
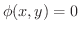 が共有点を持つときの
が共有点を持つときの 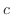 の値の極値のことです.したがって,
の値の極値のことです.したがって,  が
が
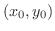 で極値をとるならば,この点において,
で極値をとるならば,この点において,
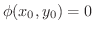 と
と
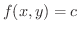 は接することになります.よって
は接することになります.よって
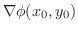 と
と
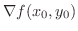 は平行となり,
は平行となり,
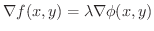
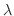 が存在するのです.
が存在するのです.
すでに外積(ベクトル積)を学んだ人は,
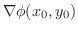 と
と
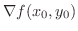 は平行より次の式を得ることができます.
は平行より次の式を得ることができます.
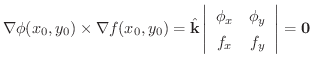
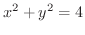 のとき,
のとき,
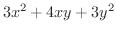 の極値を求めてみましょう.
の極値を求めてみましょう.
解
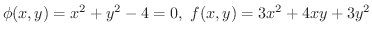 より,
より,
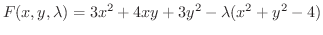
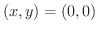 は式6.2を満たしません.そこで式6.3,6.4が
は式6.2を満たしません.そこで式6.3,6.4が
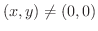 という解を持つ条件は,
という解を持つ条件は,
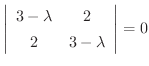
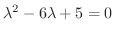 . すなわち
. すなわち
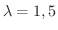 となります.
となります.
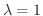 のとき,式6.2,6.3より
のとき,式6.2,6.3より
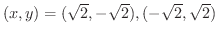 .
これらに対して,
.
これらに対して,
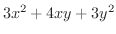 の値は
の値は 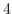 となります.
となります.
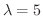 のとき,式6.2,6.3より
のとき,式6.2,6.3より
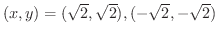 .これらに対して,
.これらに対して,
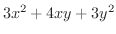 の値は
の値は 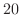 となります.
となります.
一方,
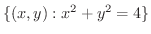 は有界閉集合であり,この上で
は有界閉集合であり,この上で
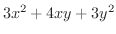 は連続なので,最大・最小値の定理より最大値,最小値をもちます.これらは極値でもあるので,上で求めた結果より,極値であれば,それは4か20のはずです.よって,最大値は20,最小値は4となります.
は連続なので,最大・最小値の定理より最大値,最小値をもちます.これらは極値でもあるので,上で求めた結果より,極値であれば,それは4か20のはずです.よって,最大値は20,最小値は4となります.

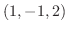 から曲面
から曲面
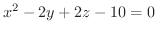 までの最短距離を求めてみましょう.
までの最短距離を求めてみましょう.
解
点 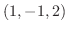 と与えられた平面上の点
と与えられた平面上の点 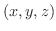 との距離を
との距離を 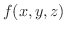 とし,
とし, 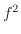 の最小値を求めます.
の最小値を求めます.
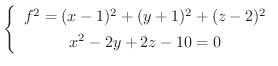
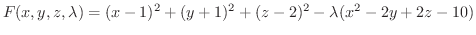
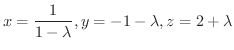
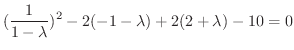
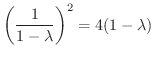
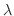 について解くと
について解くと
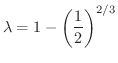
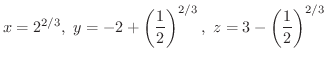
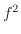 の値は,いくらでも大きい値をとることができるので,ここでの極値は極小値で,しかも唯一の極値ということから最小値となります.
の値は,いくらでも大きい値をとることができるので,ここでの極値は極小値で,しかも唯一の極値ということから最小値となります.

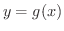 の極値を求めよう.
の極値を求めよう.
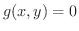 のもとでの
のもとでの  の最大値,最小値を求めよう.
の最大値,最小値を求めよう.
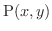 が直線
が直線
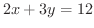 上を移動するとき,
上を移動するとき, 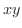 の最大値を求めよう.
の最大値を求めよう.
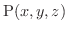 が球面
が球面
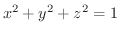 上を移動するとき,
上を移動するとき,
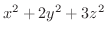 の最大値,最小値を求めよう.
の最大値,最小値を求めよう.