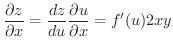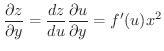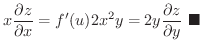Next: 2変数関数の極値(extreme values) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: gradientと方向微分(grad and directional derivatives) 目次 索引
偏微分の計算において重要な役割を果たす合成関数の微分公式を次にあげます.
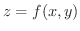 が全微分可能であり,
が全微分可能であり,
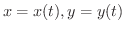 が微分可能ならば,合成関数
が微分可能ならば,合成関数
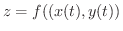 は微分可能であり,次の式が成り立つ.
は微分可能であり,次の式が成り立つ.
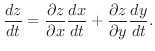
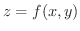 が全微分可能であり,
が全微分可能であり,
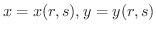 がともに微分可能ならば,合成関数
がともに微分可能ならば,合成関数
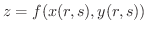 も微分可能であり,次の式が成り立つ.
も微分可能であり,次の式が成り立つ.
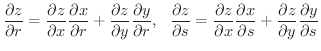
定理6.6(2)の公式を樹形図にして表わすと次の図6.6のようになります.
証明
(2)
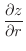 |
 |
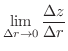 |
|
 |
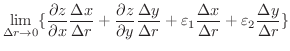 |
||
 |
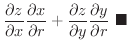 |
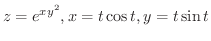 を
を  について微分してみましょう.
について微分してみましょう.
解
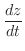 |
 |
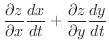 |
|
 |
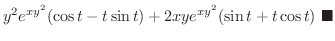 |
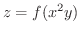 は
は
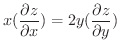 を満たすことを示してみましょう.
を満たすことを示してみましょう.
解
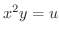 とおくと
とおくと 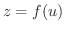 より図6.8を得ます.
より図6.8を得ます.
これより