Next: 合成関数の偏微分法(differentiation of composite functions) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 全微分(total differential) 目次 索引
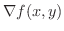 は1変数のときの導関数と同じような性質を持っています.例えば,
は1変数のときの導関数と同じような性質を持っています.例えば,
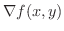 と
と
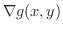 がともに存在するとき,
がともに存在するとき,
![$\nabla [f(x,y)+g(x,y)], \ \nabla [\alpha f(x,y)]$](img3488.png) ,
,
![$\nabla [f(x,y)g(x,y)]$](img3489.png) も存在し,
も存在し,
![\begin{displaymath}\begin{array}{rl}
\nabla [f(x,y)+g(x,y)] =& \nabla f(x,y) + \...
...y)] =& f(x,y) \nabla g(x,y) + g(x,y) \nabla f(x,y)
\end{array} \end{displaymath}](img3490.png)
となります.
ここでもう一度偏導関数の定義をみましょう.
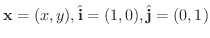 とおくと,
とおくと,
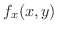 |
 |
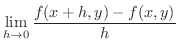 |
|
 |
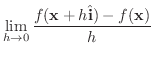 |
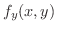 |
 |
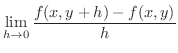 |
|
 |
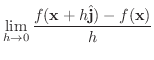 |
これから分かるように,偏導関数
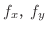 は
は
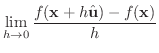
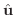 は
は
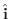 や
や
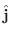 でなければならない理由はありません.そこで
でなければならない理由はありません.そこで
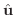 を任意の単位ベクトルとしたとき,方向微分(directional derivative) とよばれるものが定義されます.
を任意の単位ベクトルとしたとき,方向微分(directional derivative) とよばれるものが定義されます.
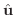 を単位ベクトルとする.次の極限値が存在するとき,その極限値を
を単位ベクトルとする.次の極限値が存在するとき,その極限値を 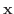 における
における
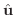 方向への
方向への  の方向微分という.
の方向微分という.
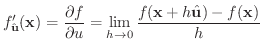
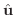 は単位ベクトルより
は単位ベクトルより
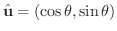 とおくこともできます.ただし
とおくこともできます.ただし 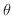 はx軸の正方向と
はx軸の正方向と
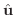 のなす角です.
のなす角です.
方向微分とgradientの間には次の定理で与えられるように密接な関係があります.
 が
が 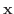 で 全微分可能ならば
で 全微分可能ならば
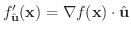
証明
 が
が 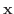 で全微分可能より
で全微分可能より
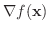 が存在し,
が存在し,
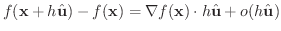
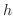 で割ると,
で割ると,
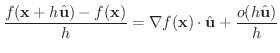
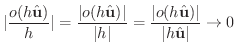
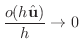
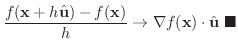
ここで
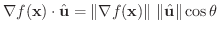 より,方向微分は
より,方向微分は
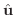 の方向が
の方向が
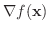 と同じ方向になったとき一番大きく,
と同じ方向になったとき一番大きく,
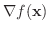 と直交したとき 0 になります.これを等高線図6.5 で考えてみましょう.
と直交したとき 0 になります.これを等高線図6.5 で考えてみましょう.
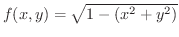 のgradientを計算すると
のgradientを計算すると
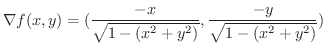
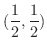 で
で
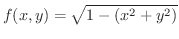 の
の
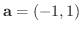 方向への方向微分を求めてみましょう.
方向への方向微分を求めてみましょう.
解
まず,方向ベクトル
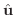 は単位ベクトルでなければならないので,
は単位ベクトルでなければならないので,
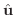 を求めると,
を求めると,
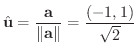
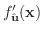 |
 |
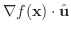 |
|
 |
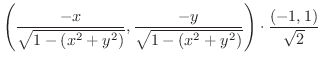 |
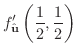 |
 |
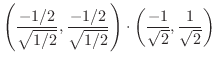 |
|
 |
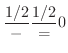 |

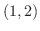 で
で 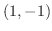 の方向に微分しよう.
の方向に微分しよう.
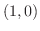 で
で
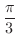 方向に微分しよう.
方向に微分しよう.
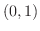 で
で 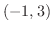 方向に微分しよう.また方向微分が最大になるような方向単位ベクトルを求めよう.
方向に微分しよう.また方向微分が最大になるような方向単位ベクトルを求めよう.
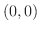 で
で
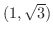 の方向に微分しよう.
の方向に微分しよう.
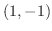 で
で
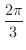 方向に微分しよう.
方向に微分しよう.
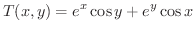
(a) 点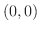 からどの方向に進むと,温度上昇が最も大きいか.また,そのときの温度の変化率を調べよう.
からどの方向に進むと,温度上昇が最も大きいか.また,そのときの温度の変化率を調べよう.
(b) 点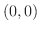 からどの方向に進むと,温度下降が最も大きいか.また,そのときの温度の変化率を調べよう.
からどの方向に進むと,温度下降が最も大きいか.また,そのときの温度の変化率を調べよう.