Next: gradientと方向微分(grad and directional derivatives) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 関数の極限(limit of function) 目次 索引
関数
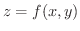 が領域
が領域 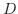 で定義されているとします.
で定義されているとします.
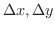 をそれぞれ
をそれぞれ の増分とするとき,これに対応する
の増分とするとき,これに対応する 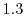 の変動量
の変動量
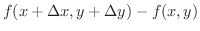 を
を 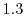 の増分といい,
の増分といい, 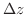 で表わします.
ここで,
で表わします.
ここで,
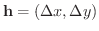 とおき,
とおき,
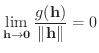
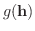 を o(h) で表わすとします.このとき,
を o(h) で表わすとします.このとき,
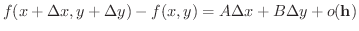
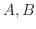 が存在するとき,関数
が存在するとき,関数  は点
は点 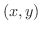 で全微分可能(totally differentiable) であるといいます.ちょっと分りにくいですね.そこで,全微分可能のときどんなことがいえるのか調べてみましょう.
で全微分可能(totally differentiable) であるといいます.ちょっと分りにくいですね.そこで,全微分可能のときどんなことがいえるのか調べてみましょう.
 が点
が点
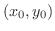 で全微分可能ならば,
で全微分可能ならば,  は点
は点
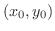 で連続かつ偏微分可能であり,
で連続かつ偏微分可能であり,
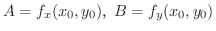 が成り立つ.
が成り立つ.
証明 点
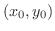 で全微分可能なとき,
で全微分可能なとき,
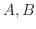 が存在する.よって
が存在する.よって
![$\displaystyle \lim_{{\bf h} \rightarrow {\bf0}}[f(x_{0} + \Delta x, y_{0} + \Delta y) - f(x_{0},y_{0})] = 0$](img3394.png)
 は点
は点
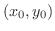 で連続.次に,式6.1 で
で連続.次に,式6.1 で
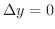 とおくと,
とおくと,
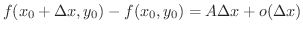
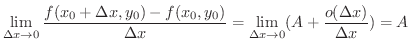
 は点
は点
 で
で  について偏微分可能で,
について偏微分可能で,
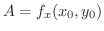 である.同様にして,
である.同様にして,
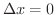 のときを考えることにより,
のときを考えることにより,  は点
は点
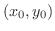 で
で  について偏微分可能で,
について偏微分可能で,
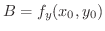 を得る.
を得る.

 は全微分可能か調べてみましょう.
は全微分可能か調べてみましょう.
解
例題6.2より  は
は  で偏微分可能となりますが,例題6.3より
で偏微分可能となりますが,例題6.3より  で連続ではありません.よって定理6.4より
で連続ではありません.よって定理6.4より  は
は  で全微分可能ではありません.
で全微分可能ではありません.

この例題からも分かるように,偏微分可能であることは全微分可能であることの十分条件ではありません.何が足りないのか考えてみましょう.
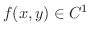 級 ならばどうでしょうか.
級 ならばどうでしょうか.
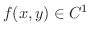 級 とすると
級 とすると
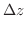 |
 |
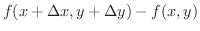 |
|
 |
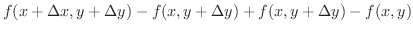 |
||
 |
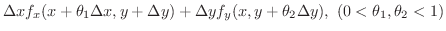 |
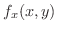 は連続なので,
は連続なので,
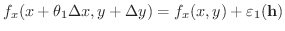
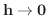 のとき
のとき
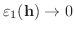 .
同様に,
.
同様に,
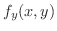 も連続なので,
も連続なので,
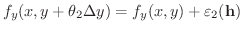
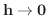 のとき
のとき
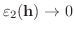 .
よって,
.
よって,
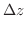 |
 |
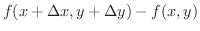 |
|
 |
![$\displaystyle [f_{x}(x,y) + \varepsilon_{1}({\bf h})]\Delta x + [f_{y}(x,y) + \varepsilon_{2}({\bf h})]\Delta y$](img3411.png) |
||
 |
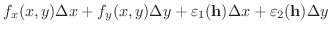 |
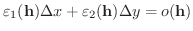 を示しましょう.
を示しましょう.
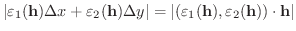
 の間に
の間に
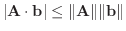
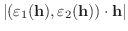 |
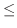 |
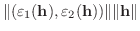 |
|
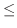 |
![$\displaystyle [\vert\varepsilon_{1}({\bf h})\vert + \vert\varepsilon_{2}({\bf h})\vert]\Vert{\bf h}\Vert = o({\bf h})$](img3419.png) |
このことより,次の定理を得ます.
 が
が 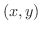 の近傍で
の近傍で 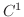 級 ならば,
級 ならば,  は
は 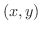 で全微分可能である.
で全微分可能である.
 が全微分可能なとき,
が全微分可能なとき,
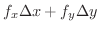 は
は 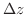 の主要な部分とみなせるので,これを点
の主要な部分とみなせるので,これを点 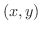 における関数
における関数
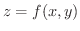 の 全微分(total differential) といい
の 全微分(total differential) といい 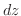 または
または 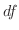 で表わします.つまり
で表わします.つまり
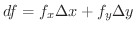
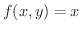 および
および
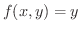 を考えることにより,
を考えることにより,
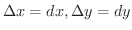 とおけるので
とおけるので
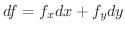
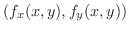 を
を  の 勾配(gradient) といい,
の 勾配(gradient) といい,
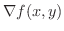 で表わします.つまり
で表わします.つまり
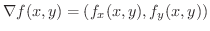
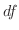 は
は 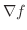 を用いて次のように表わすことができます.
を用いて次のように表わすことができます.
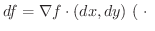 は内積
は内積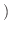
ここにでてきたベクトル
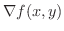 は2変数のベクトル関数となり,ベクトル場(vector field) といいます.
は2変数のベクトル関数となり,ベクトル場(vector field) といいます.
次に,点
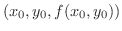 を通り法線ベクトルが
を通り法線ベクトルが
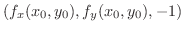 であたえられる平面を考えます.このとき,平面上の任意の点
であたえられる平面を考えます.このとき,平面上の任意の点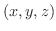 と点
と点
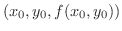 が作るベクトルと法線ベクトルは直交します.したがって,
が作るベクトルと法線ベクトルは直交します.したがって,
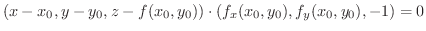
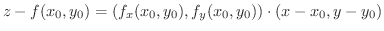
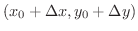 に対応する
に対応する は
は
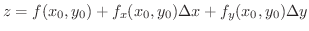
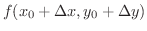 の近似となります.このような平面を,接平面(tangent plane)といいます.また,法線ベクトルは
の近似となります.このような平面を,接平面(tangent plane)といいます.また,法線ベクトルは
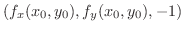 で与えられます.
で与えられます.
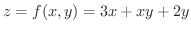 の点
の点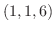 における接平面と法線を求めてみましょう.
における接平面と法線を求めてみましょう.
解
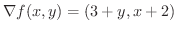 より
より
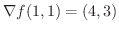 . これより接平面の方程式は
. これより接平面の方程式は
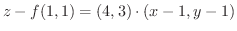
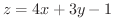 .また,法線は
.また,法線は
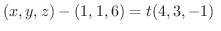 または
または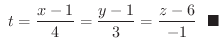
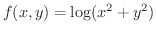 の全微分と
の全微分と 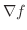 を求めてみましょう.
を求めてみましょう.
解
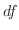 |
 |
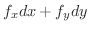 |
|
 |
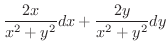 |
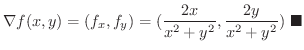
![$\displaystyle{\sqrt{27}\sqrt[3]{1021}}$](img3454.png) を近似してみましょう.
を近似してみましょう.
解
電卓,コンピュータソフトを用いれば,簡単に近似できますが,手もとにそういう道具がないときはこんなふうにして求めます.
まず,関数
![$f(x,y) = \sqrt{x} \sqrt[3]{y}$](img3455.png) を考えます.このとき,
を考えます.このとき,
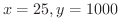 ならば,
ならば,
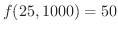 と求めることができます.そこで,
と求めることができます.そこで,
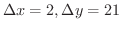 とおくと,求める値は
とおくと,求める値は
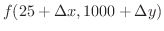 となります.ここで,
となります.ここで,
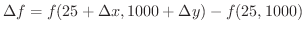
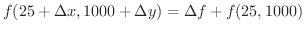
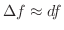 なので,
なので,
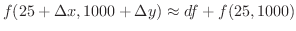
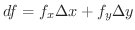 より
より
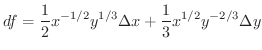
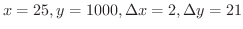 のとき,
のとき,
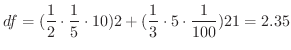
![$\displaystyle \sqrt{27}\sqrt[3]{1021} \approx \sqrt{25}\sqrt[3]{1000} + 2.35 = 52.35 $](img3468.png)
![$\sqrt{27}\sqrt[3]{1021}$](img3469.png) をMathematicaを用いて求めると52.32となります.
をMathematicaを用いて求めると52.32となります.

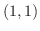 に対応する点を通る接平面と法線を求めよう.
に対応する点を通る接平面と法線を求めよう.