Next: 全微分(total differential) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 偏導関数(partial derivatives) 目次 索引
関数
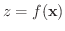 において,
において,
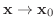 のとき,
のとき,
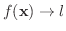 ならば,
ならば, 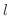 を
を 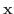 が
が
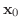 に近づくときの
に近づくときの
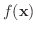 の極限値といい,
の極限値といい,
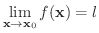
1変数のときと違い
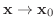 を満たす近づき方は無限にあります.上の定義は
を満たす近づき方は無限にあります.上の定義は
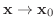 を満たすすべての近づき方に対して,
を満たすすべての近づき方に対して,
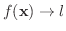 であるといっているのです.
であるといっているのです.
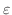 に対して,
に対して,
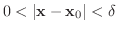 のとき,
のとき,
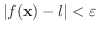 が成り立つように正の数
が成り立つように正の数 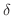 が選べるなら
が選べるなら
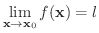
この定義にでてきた
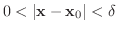 は 2変数のときは
は 2変数のときは
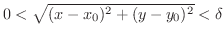 と表わされ,半径
と表わされ,半径 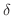 の円の中心
の円の中心
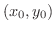 を除いた部分であることがわかります.このような集合を点
を除いた部分であることがわかります.このような集合を点
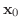 の
の 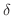 近傍といい,
近傍といい,
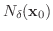 で表わします.
で表わします.
ここで,平面上の点についての理解を深めておきます.
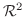 のある部分集合を
のある部分集合を  とします.このとき平面上の点
とします.このとき平面上の点 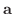 は次の3種類に分類されます.
は次の3種類に分類されます.
(1)
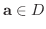 に対し,
に対し,
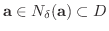
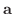 の
の 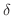 近傍が存在するとき,
近傍が存在するとき, 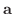 は
は  の 内点(interior point) といいます.
の 内点(interior point) といいます.
(2)
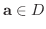 に対し,
に対し,
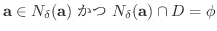
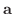 の
の 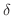 近傍が存在するとき,
近傍が存在するとき, 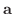 は
は  の 外点(exterior point) といいます.
の 外点(exterior point) といいます.
(3) 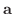 が
が  の内点でも外点でもないとき,点
の内点でも外点でもないとき,点 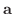 を
を  の 境界点(boundary point) といいます.
の 境界点(boundary point) といいます.
 の境界点すべての集合を
の境界点すべての集合を  の 境界(boundary) といい,
の 境界(boundary) といい,
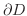 で表わします.また,すべての点が
で表わします.また,すべての点が  の内点のとき
の内点のとき  を 開集合(open set) といいます.
を 開集合(open set) といいます.
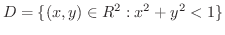 は開集合であることを示してみましょう.
は開集合であることを示してみましょう.
解
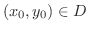 を
を  の任意の点とします.このとき原点と点
の任意の点とします.このとき原点と点
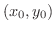 までの距離を求めると
までの距離を求めると
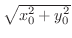 となります.よって,
となります.よって, 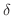 を
を
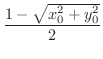 より小さくとれば,
より小さくとれば,
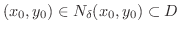
 は開集合となります.
は開集合となります.

また,集合  の補集合
の補集合 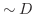 が開集合のとき
が開集合のとき  を 閉集合(closed set) といいます.
を 閉集合(closed set) といいます. にその境界
にその境界
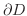 を付加してできる集合を 閉包(closure) といい,
を付加してできる集合を 閉包(closure) といい,
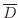 で表わします.
で表わします.
集合  に属するどの2点も,
に属するどの2点も,  の中だけを通る連続曲線で結ぶことができるとき,
の中だけを通る連続曲線で結ぶことができるとき,  を 連結(connected)な集合といいます.また,連結な開集合を 領域(region) といいます.領域
を 連結(connected)な集合といいます.また,連結な開集合を 領域(region) といいます.領域  の閉包
の閉包
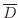 を 閉領域(closed region) といいます.
を 閉領域(closed region) といいます.
集合  が半径
が半径 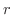 の開円板
の開円板
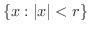 に含まれるとき,集合
に含まれるとき,集合  は 有界(bounded) であるといいます.
は 有界(bounded) であるといいます.
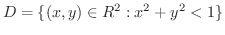
解 境界は
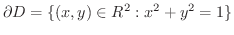
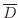 は
は
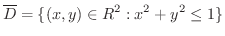
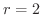 とおくと,
とおくと,
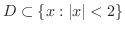 となるので,
となるので,  は有界です.最後に
は有界です.最後に  に属するどの2点も半径1の円の中にあるので,直線(連続曲線)で結ぶことができます.よって領域となります.
に属するどの2点も半径1の円の中にあるので,直線(連続曲線)で結ぶことができます.よって領域となります.

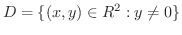
解
 は平面から
は平面から  軸を除いた点の集合です.よって,どんな半径の開円板をとっても
軸を除いた点の集合です.よって,どんな半径の開円板をとっても  を含むことができません.また,上半平面と下半平面から,1点ずつとると,この2点はどんな連続曲線でも結ぶことができません.よって領域ではありません.
を含むことができません.また,上半平面と下半平面から,1点ずつとると,この2点はどんな連続曲線でも結ぶことができません.よって領域ではありません.

集合上での点についてはこのくらいにして,話を関数の極限にもどします.まず例として次の極限値の問題を考えてみましょう.
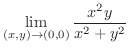
解
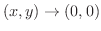 のとき,
のとき,
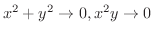 となります.では,どちらが速く0に近づくのでしょうか.それを調べるために,分母のそれぞれの項の中で最小な次数と分子のそれぞれの項の中で最小な次数とを比較します(なぜなら,次数が大きいほど速く0に近づきます).この場合は,分子の項の最小次数は3で,分母の項の最小次数は2です.このように分子の項の最小次数
となります.では,どちらが速く0に近づくのでしょうか.それを調べるために,分母のそれぞれの項の中で最小な次数と分子のそれぞれの項の中で最小な次数とを比較します(なぜなら,次数が大きいほど速く0に近づきます).この場合は,分子の項の最小次数は3で,分母の項の最小次数は2です.このように分子の項の最小次数 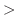 分母の項の最小次数のときは,平面上の任意の点
分母の項の最小次数のときは,平面上の任意の点 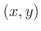 を
を
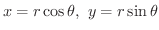
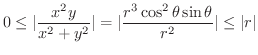
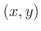 がどのように
がどのように 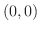 に近づいても,原点と点
に近づいても,原点と点 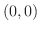 の距離
の距離
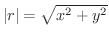 は 0 に近づくので,
は 0 に近づくので,
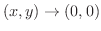 と
と
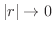 は同値です.よって,はさみうちの定理より,
は同値です.よって,はさみうちの定理より,
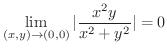
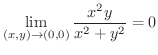

もう1つ極限値の問題を解いてみましょう.
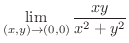
解
この例では分子の項の最小次数 = 分母の項の最小次数となります.ここで, 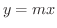 とおくと,
とおくと,
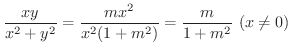
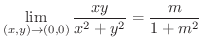
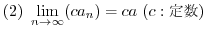 の値によって,つまり,
の値によって,つまり, 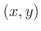 が
が 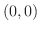 に近づく経路によって異なります.よって上の定義より
に近づく経路によって異なります.よって上の定義より
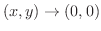 のとき極限値は存在しません.
のとき極限値は存在しません.

1変数のときと同様,
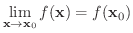
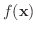 は
は
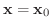 で連続であるといいます.また,ある集合
で連続であるといいます.また,ある集合  の各点で連続のとき,
の各点で連続のとき,
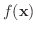 は
は  で連続であるといいます.
で連続であるといいます.
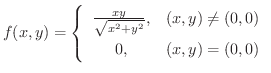
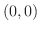 における連続性を調べてみましょう.
における連続性を調べてみましょう.
解
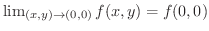 が成り立つか調べればよいでしょう.分子の項の最小次数
が成り立つか調べればよいでしょう.分子の項の最小次数 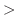 分母の項の最小次数より,
分母の項の最小次数より,
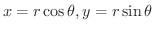 とおくと,
とおくと,
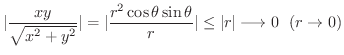
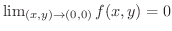 . また,
. また,
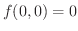 より,
より, 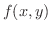 は
は 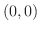 で連続であることがわかります.
で連続であることがわかります.

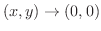 のとき,次の関数の極限値を求めよう.
のとき,次の関数の極限値を求めよう.
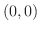 における連続性を調べよう.
における連続性を調べよう.