Next: 関数の極限(limit of function) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 関数の定義(definition of functions) 目次 索引
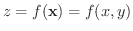 について点
について点
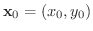 で次のような極限を考えます.
で次のような極限を考えます.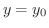 をー定にして,
をー定にして,  の関数
の関数
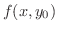 が
が  で微分可能なとき,つまり
で微分可能なとき,つまり
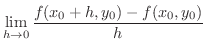
 は点
は点
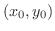 で
で  に関して偏微分可能(partially differentiable) であるといいます.また,この極限値を
に関して偏微分可能(partially differentiable) であるといいます.また,この極限値を  に関する偏微分係数といい,
に関する偏微分係数といい,
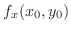 で表わします.
で表わします. の代わりに
の代わりに  を一定にして考えると,上と同じようにして,
を一定にして考えると,上と同じようにして,  に関しての偏微分可能性,偏微分係数が定義されます.また,集合
に関しての偏微分可能性,偏微分係数が定義されます.また,集合 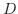 の各点で
の各点で 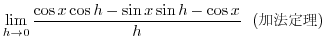 に関して偏微分可能のとき
に関して偏微分可能のとき  は
は 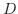 で偏微分可能であるといいます.
で偏微分可能であるといいます.
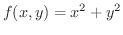 の偏微分係数
の偏微分係数
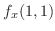 を求めてみましょう.
を求めてみましょう.
解
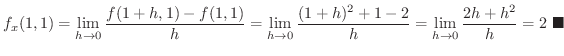
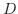 の各点
の各点
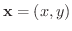 に,その点における
に,その点における  に関する偏微分係数を対応させることにより得られる関数を
に関する偏微分係数を対応させることにより得られる関数を
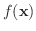 の
の  に関する偏導関数(partial derivative) といい,
に関する偏導関数(partial derivative) といい,
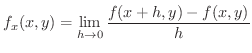
 に関する偏導関数を
に関する偏導関数を
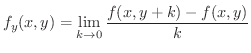
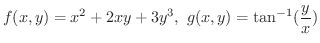
解
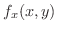 を求めるには,
を求めるには,  を定数と考えて,
を定数と考えて,  を
を  について微分します.
について微分します.
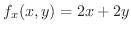
 を定数と考えて
を定数と考えて について微分すると
について微分すると
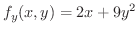
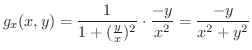
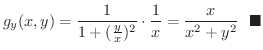
これから分かるように1変数の導関数が求められれば,何の問題もなく2変数の偏導関数が求められます.
偏導関数
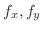 がさらに偏微分可能なとき,それらの偏導関数を 第2次偏導関数(2nd partial derivatives) といい,
がさらに偏微分可能なとき,それらの偏導関数を 第2次偏導関数(2nd partial derivatives) といい,
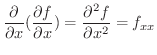
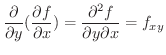
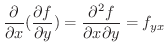
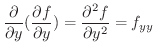
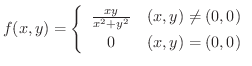 のとき
のとき
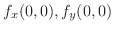 を求め,
を求め, 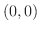 で偏微分可能か調べてみましょう.
で偏微分可能か調べてみましょう.
解を見る前にある学生の解答をみてみましょう.
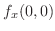 を求めればよいので,まず,
を求めればよいので,まず,
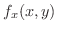 を求めます.
を求めます.
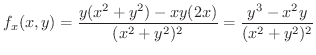
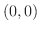 を代入すると
を代入すると
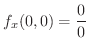
残念ながら,この学生の解答は正解ではありません(なぜでしょう?).正解をみてみましょう.
解
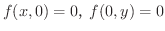 より
より
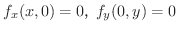 となるので,
となるので,  は点
は点 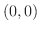 で偏微分可能となります.
で偏微分可能となります.

2次以上の偏導関数を高次偏導関数といいます.高次偏導関数では,微分する順序に注意しなければならないことがあります.つまり,関数  について常に
について常に
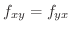 が成り立つとは限りません.次の例題は
が成り立つとは限りません.次の例題は
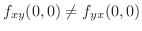 を示すのに,よく用いられる例題です.
を示すのに,よく用いられる例題です.
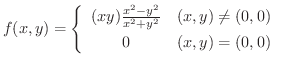 のとき,
のとき,
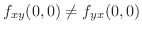 を示してみましょう.
を示してみましょう.
解
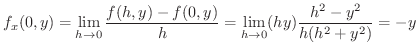
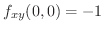 . 次に,
. 次に,
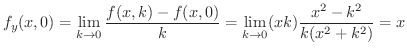
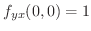 .
.

このように 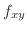 と
と 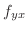 はいつも等しいとは限りません.そこで
はいつも等しいとは限りません.そこで
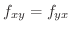 が成り立つための十分条件(この条件のもとなら必ず成り立つという条件)を述べておきます.その前に,ちょっと準備をします.
が成り立つための十分条件(この条件のもとなら必ず成り立つという条件)を述べておきます.その前に,ちょっと準備をします.
 が領域
が領域 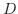 で第
で第 次までの偏導関数をもち,かつそれらがすべて連続なとき,
次までの偏導関数をもち,かつそれらがすべて連続なとき,  は
は 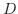 で
で 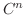 級であるといいます.
級であるといいます.
準備ができたので,
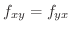 が成り立つための十分条件を示してみましょう.
が成り立つための十分条件を示してみましょう.
 が領域
が領域 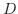 で
で 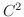 級であるならば,
級であるならば,
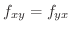 である.
である.
証明 偏導関数の定義と平均値の定理をつかって証明できるので,各自に任せる.