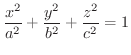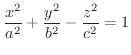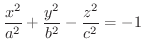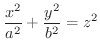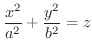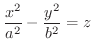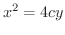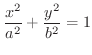関数の定義(definition of functions)

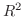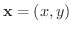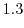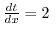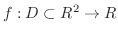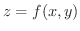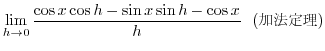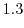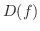平面 ${R}^{2}$ の部分集合に属する各点 ${\bf x} = (x,y)$ に対して，実数が1つ定まるような規則をから ${\mathcal R}$ への2変数関数といい， $f:D \subset R^2 \rightarrow R$ またはで表わします．このときを独立変数，を従属変数といいます．またこのようなを関数の 定義域(domain) といいで表わします．つまり，

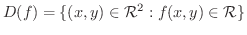
$\displaystyle D(f) = \{(x,y) \in {\mathcal R}^{2} : f(x,y) \in {\mathcal R}\}$

また，

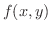を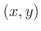

の 像(image) といい，その集合は 値域(range) といい

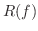で表わします．つまり，

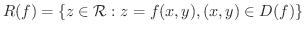
$\displaystyle R(f) = \{z \in {\mathcal R} : z = f(x,y), (x,y) \in D(f) \}$

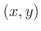の像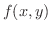

を空間上に描いたものを関数

の グラフ(graph) といい，

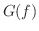で表わします．つまり，

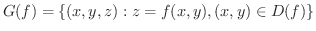
$\displaystyle G(f) = \{(x,y,z) : z = f(x,y), (x,y) \in D(f) \}$

よって2変数関数のグラフは曲面を表わします．

例題 6..1

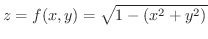$\displaystyle{z = f(x,y) = \sqrt{1-(x^2 + y^2)}}$ の定義域を求め，

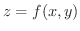のグラフを描いてみましょう．

解まず，定義域は

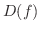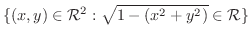$\displaystyle D(f)$	$\displaystyle =$	$\displaystyle \{(x,y) \in {\mathcal R}^2 : \sqrt{1 - (x^2 + y^2)} \in {\mathcal R} \}$
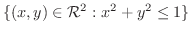	$\displaystyle =$	$\displaystyle \{(x,y) \in {\mathcal R}^2 : x^2 + y^2 \leq 1 \}$

となります．

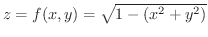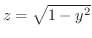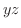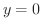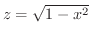$z = f(x,y) = \sqrt{1 - (x^2 + y^2)}$ のグラフは次のように描きます．まず，とおくと $z = \sqrt{1 - y^2}$ となり，平面上でのグラフを得ます．次に，とおくと $z = \sqrt{1 - x^2}$ となり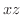，平面上でのグラフを得ます．最後に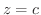，とおくと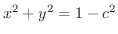となり，平面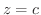上でのグラフを得ます．この平面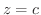上のグラフを 等高線(level curve) といいます．これらの情報よりグラフを描きます．

**図 6.1:** f(x,y)のグラフ
$\begin{figure}\vskip -1cm \begin{center} \includegraphics[width=7cm]{CALCFIG/Fig6-1-1.eps} \end{center}\vskip -2cm \end{figure}$

ただ，一般に2変数関数のグラフは難しすぎて，描けないことがしばしばあります．これが3変数関数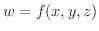となると，グラフを描くには4次元の空間が必要となるため描けません．そこで3変数関数はどんな行動をとるのか，等位面(level surface) とよばれるものをもちいて調べます．等位面とは

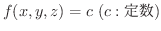
$\displaystyle f(x,y,z) = c \ (c : 定数)$

を満たす点

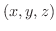の集まりのことです．つまり

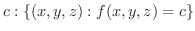
$\displaystyle c : \{(x,y,z) : f(x,y,z) = c \}$

このとき，この等位面を等位

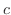の等位面といいます．等高線でも同じことがいえます．

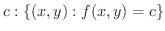
$\displaystyle c : \{(x,y) : f(x,y) = c \}$

で等高線が与えられるとき，この等高線を高度

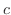の等高線といいます．

2次曲面 1変数の関数は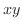平面を用いて表しましたが，2変数の関数は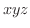空間を用いて表わすことを学びました．そこで，ここでは，次の2次式で表される曲面について分類します．

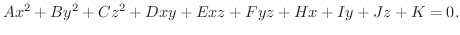
$\displaystyle Ax^{2} + By^{2} + Cz^{2} + Dxy + Exz + Fyz + Hx + Iy + Jz + K = 0.$

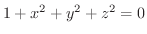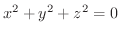適当な変数変換により，非退化な2次式は次の9個の型に分類されます．ここで，退化な2次式とは， $1 + x^{2} + y^{2} + z^{2} = 0$ や $x^{2} + y^{2} + z^{2} = 0$ のように，式を満たす点が無い場合や1点しか無い場合をいいます．

楕円面(ellipsoid) $\displaystyle{\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1}$
1葉双曲面(hyperboloid of one sheet) $\displaystyle{\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} - \frac{z^{2}}{c^{2}} = 1}$
2葉双曲面(hyperboloid of two sheet) $\displaystyle{\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} - \frac{z^{2}}{c^{2}} = -1}$
2次錐面(quadric cone) $\displaystyle{\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = z^{2}}$
楕円放物面(elliptic paraboloid) $\displaystyle{\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = z}$
双曲放物面(hyperbolic paraboloid) $\displaystyle{\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = z}$
放物柱(parabolic cylinder) $\displaystyle{x^{2} = 4cy}$
楕円柱(elliptic cylinder) $\displaystyle{\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1}$
双曲柱(hyperbolic cylinder) $\displaystyle{\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1}$

確認問題

1.

次の関数の定義域と値域を求めよう．

(a) $\displaystyle{f(x,y) = \sqrt{xy}}$ (b) $\displaystyle{f(x,y) = \frac{1}{x+y}}$ (c) $\displaystyle{f(x,y) = \frac{1}{x^{2} + y^{2}}}$

(d) $\displaystyle{f(x,y) = \frac{x^{2}}{x^{2} + y^{2}}}$ (e) $\displaystyle{f(x,y) = \log(1-xy)}$ (f) $\displaystyle{f(x,y,z) = \frac{z}{x^{2} - y^{2}}}$

2.

次の曲面を分類しよう．

(a) $\displaystyle{x^{2} + 4y^{2} - 16z^{2} = 0}$ (b) $\displaystyle{x^{2} + 4y^{2} + 16z^{2}- 12 = 0}$ (c) $\displaystyle{x - 4y^{2} = 0}$

(d) $\displaystyle{x^{2} - 4y^{2} - 2z = 0}$ (e) $\displaystyle{2x^{2} + 4y^{2} - 1 = 0}$ (f) $\displaystyle{x^{2} + 4y^{2} - 4z = 0}$

(g) $\displaystyle{2x^{2} - 4y^{2} - 6 = 0}$ (h) $\displaystyle{x^{2} + y^{2} - 2z^{2} -10 = 0}$ (i) $\displaystyle{x^{2} + y^{2} - 2z^{2} +10 = 0}$

演習問題

1.: 次の関数の定義域をもとめそのグラフを描こう．
(a) $\displaystyle{f(x,y) = x^2 - y^2}$ (b) $\displaystyle{f(x,y) = \frac{x^2}{x^2 + y^2}}$ (c) $\displaystyle{f(x,y) = \log{(1 - xy)}}$