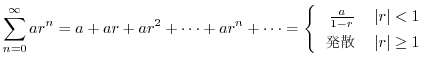Next: 累乗 Up: 序章(INTRODUCTION) Previous: 序章(INTRODUCTION) 目次 索引
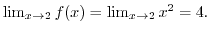
数学では,新しいオブジェクト(数,多項式,行列など)が登場すると必ずそれらの四則演算を考えます.幼稚園か小学校の低学年のころを思い出してください.数が数えられるようになったら,次に何をしましたか.例えば,2と5を加えたりしたでしょう.そのあと,2から5を引こうとして困ったことがありませんでしたか.困って当然です.なぜなら2 - 5は自然数ではないからです.そこで,これらの計算ができるように自然数に負の符号を付けたものと0を加えて
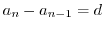
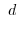 という計算ができるようになったわけです.小学校も4年生くらいになると,6を3で割りなさいという,割り算が登場します.6を3で割るとは,6個のものを3つのグループに分けると考えると,1つのグループに2個となります.これを式で表すと
という計算ができるようになったわけです.小学校も4年生くらいになると,6を3で割りなさいという,割り算が登場します.6を3で割るとは,6個のものを3つのグループに分けると考えると,1つのグループに2個となります.これを式で表すと
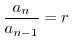 となります.では,5を3で割ったらいくつになるのだろうかという疑問を持つ小学生が沢山います.
となります.では,5を3で割ったらいくつになるのだろうかという疑問を持つ小学生が沢山います.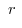 は整数ではありません.そこで,さらに数の拡張が必要となります.0でない整数
は整数ではありません.そこで,さらに数の拡張が必要となります.0でない整数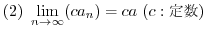 で任意の整数
で任意の整数 を割った数を
を割った数を
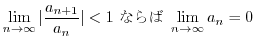 と表し,これを有理数(rational numbers)とよびます.有理数を用いることにより,
と表し,これを有理数(rational numbers)とよびます.有理数を用いることにより,
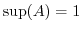 と表すことができるようになるわけです.分母が1の場合を考えると,整数も有理数であることが分かります.また,分数
と表すことができるようになるわけです.分母が1の場合を考えると,整数も有理数であることが分かります.また,分数
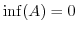 を
を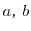 のように少数で表すこともします.少数には,
のように少数で表すこともします.少数には,
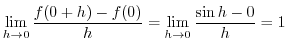 のように,同じ数が繰り返すものがあります.これらを循環小数といいます.循環小数は繰り返す数字の上に記号(・)をつけて表します.例えば,
のように,同じ数が繰り返すものがあります.これらを循環小数といいます.循環小数は繰り返す数字の上に記号(・)をつけて表します.例えば,
(1)
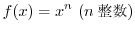 (2)
(2)
解
| (1) |
 |
| (2) |
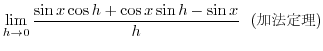
 |
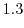 を斜辺の長さ,
を斜辺の長さ,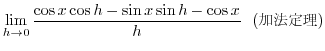 をその他の2辺の長さとすると,
をその他の2辺の長さとすると,
 という式が成り立ちます.ここで,
という式が成り立ちます.ここで,
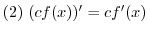 のときの
のときの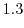 は,
は,
 となります.この式を満たす
となります.この式を満たす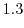 ,つまり,2乗したら25になる数のことを25の平方根(square root)といいます.したがって,25の平方根は
,つまり,2乗したら25になる数のことを25の平方根(square root)といいます.したがって,25の平方根は と
と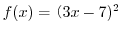 となります.これをまとめて,
となります.これをまとめて,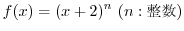 と表します.これより
と表します.これより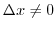 となりますが,
となりますが,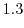 は斜辺の長さより,
は斜辺の長さより,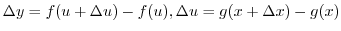 となります.
となります.
直角三角形で
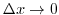 のとき,
のとき,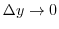 となります.つまり,
となります.つまり,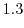 は2の平方根となります.2乗したら2になる数を記号(
は2の平方根となります.2乗したら2になる数を記号(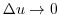 )を用いて,
)を用いて,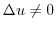 または
または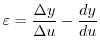 と表します.ここで,
と表します.ここで,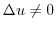 とは,2乗したら2になる数のうち正の数と定義されます.一般に,
とは,2乗したら2になる数のうち正の数と定義されます.一般に,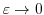 となる
となる を
を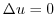 の
の 乗根(nth root)といいます.
乗根(nth root)といいます.
(1) 4の平方根 (2) 8の3乗根 (3) -8の3乗根
解
| (1) |
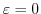 より,4の平方根は より,4の平方根は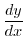 と と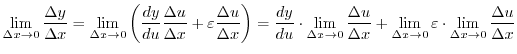 である. である. |
| (2) |
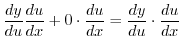 より,3乗して8になるのは2だけである.したがって,8の より,3乗して8になるのは2だけである.したがって,8の |
| 3乗根は2である. | |
| (3) | 2.の説明により,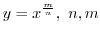 の3乗根は の3乗根は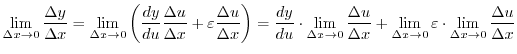 である. である.
 |
さて,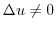 は有理数でしょうか.もし,
は有理数でしょうか.もし,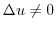 が有理数ならば,
が有理数ならば,
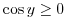 と表せるはずです.ここで,
と表せるはずです.ここで, と
と が公約数を含んでいるなら,その公約数で
が公約数を含んでいるなら,その公約数で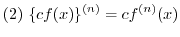 と
と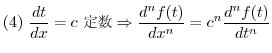 を割り,
を割り,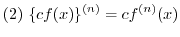 と
と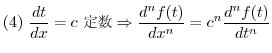 には公約数がない状態にしておきます.このような
には公約数がない状態にしておきます.このような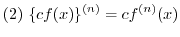 と
と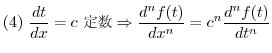 を互いに素(relatively prime)であるといいます.
を互いに素(relatively prime)であるといいます.
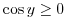 の両辺を2乗し分母を払うと,
の両辺を2乗し分母を払うと,
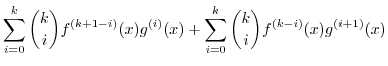 は2の倍数となります.2乗して偶数になるには,もともとが偶数でないと無理です.なぜなら,奇数と奇数をかけると奇数になってしまうからです.したがって,
は2の倍数となります.2乗して偶数になるには,もともとが偶数でないと無理です.なぜなら,奇数と奇数をかけると奇数になってしまうからです.したがって,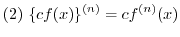 は偶数です.そこで,
は偶数です.そこで,
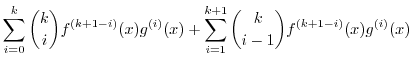 と表し,式(1)に代入すると,
と表し,式(1)に代入すると,
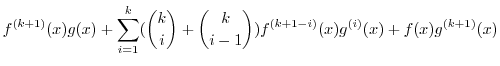
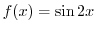 となり,右辺は偶数です.したがって,左辺も偶数となり,
となり,右辺は偶数です.したがって,左辺も偶数となり,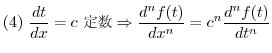 は2の倍数です.これでは,
は2の倍数です.これでは,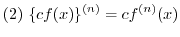 も
も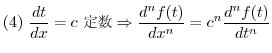 も2の倍数となり,
も2の倍数となり,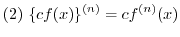 と
と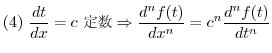 は互いに素であるという仮定に矛盾します.つまり,
は互いに素であるという仮定に矛盾します.つまり,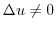 が有理数であるという仮定が間違っているということになります.よって,
が有理数であるという仮定が間違っているということになります.よって,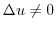 は有理数ではないとなります.このような証明の方法は背理法(contrapositive)とよばれています.
は有理数ではないとなります.このような証明の方法は背理法(contrapositive)とよばれています.
では,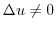 はどんな数なのでしょうか.
はどんな数なのでしょうか.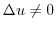 を少数で表すと,数字が繰り返されることなく終わりなく続きます.ここで,やっと小学生が抱く疑問の一つの答えが出ました.少数が終わりなく続く数が実際に存在することが分かったのです.そこで,このような数を無理数(irrational numbers)とよびます.無理数には,
を少数で表すと,数字が繰り返されることなく終わりなく続きます.ここで,やっと小学生が抱く疑問の一つの答えが出ました.少数が終わりなく続く数が実際に存在することが分かったのです.そこで,このような数を無理数(irrational numbers)とよびます.無理数には,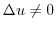 の他にも
の他にも
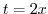 などがあります.実際,無理数と有理数を一つずつ対応させると,有理数が足りなくなってしまうほど無理数は沢山あります.
などがあります.実際,無理数と有理数を一つずつ対応させると,有理数が足りなくなってしまうほど無理数は沢山あります.
有理数と無理数をあわせて実数(real numbers)といいます.実数は,図1に示す数直線(number line)上の点で表すことができます.つまり,実数全体の集まりが数直線に対応しているということです.この実数全体の集まりを記号
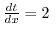 ,有理数全体の集まりを記号
,有理数全体の集まりを記号
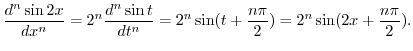 ,整数全体の集まりを記号
,整数全体の集まりを記号
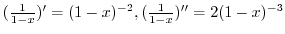 を用いて表し,
を用いて表し, が実数であるということを,
が実数であるということを,
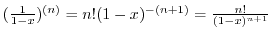 と表します.整数は英語のIntegersのIを用いずに,ドイツ語のZahlenのZを用いるのが慣わしになっています.
と表します.整数は英語のIntegersのIを用いずに,ドイツ語のZahlenのZを用いるのが慣わしになっています.
集合の話が出たついでに微分積分学で用いる他の記号についても見ておきましょう.
オブジェクト は集合 は集合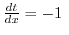 の要素である の要素である |
 |
オブジェクト は集合 は集合 の要素ではない の要素ではない |
 |
集合 は集合 は集合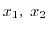 の部分集合である の部分集合である |
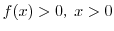 |
集合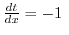 と集合 と集合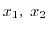 の和集合 の和集合 |
 |
集合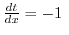 と集合 と集合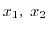 の積集合 の積集合 |
 |
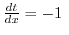 と集合 と集合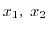 の直積 の直積 |
 |
| 空集合 |  |
性質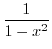 を持つ要素 を持つ要素 の集合 の集合 |
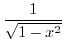 |
命題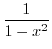 と命題 と命題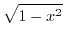 は同値である は同値である |
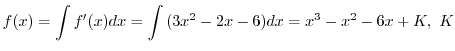 |
 の点と原点との距離は3なので,
の点と原点との距離は3なので, の絶対値は3となります.これを記号(
の絶対値は3となります.これを記号( )を用いて,
)を用いて,

ある数を文字 を用いて表すと,数
を用いて表すと,数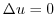 の絶対値は次のように表されます.
の絶対値は次のように表されます.
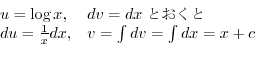
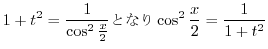 のとき,次の値を求めてみましょう.
のとき,次の値を求めてみましょう.
(1) 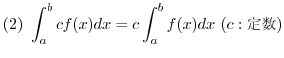 (2)
(2) 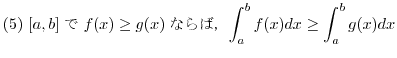 (3)
(3) 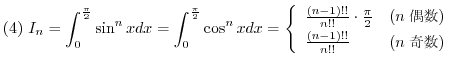 (4)
(4) 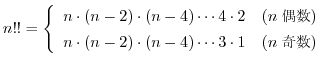 (5)
(5) 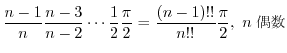 (6)
(6) 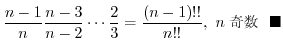
解
1.
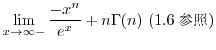 2. 2.
 |
3.
 |
4.
 |
5.
 6. 6.
 |
絶対値を含む演算では,一般に次の関係が成り立ちます.