Next: 不等式 Up: 序章(INTRODUCTION) Previous: 数(NUMBERS) 目次 索引
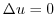 を3回かけあわせたとすると,「
を3回かけあわせたとすると,「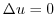 の3乗」といい,
の3乗」といい,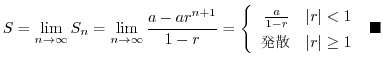 と表します.このとき,
と表します.このとき,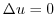 を底(base)テイといい,かけた回数を添え字として右肩に小さく書き指数(exponent)といいます.
を底(base)テイといい,かけた回数を添え字として右肩に小さく書き指数(exponent)といいます.
(1)
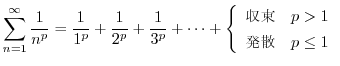
解
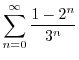

累乗どうしの掛け算はそれほど難しくはありません.例えば,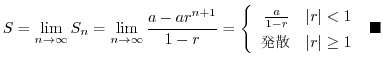 と
と をかけると,
をかけると,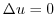 を3回と4回の合計7回かけることになるので,
を3回と4回の合計7回かけることになるので,
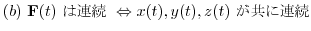
 で
で が整数のとき,
が整数のとき,
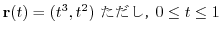
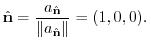 を
を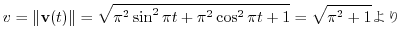 で割ってみましょう.
で割ってみましょう.
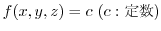
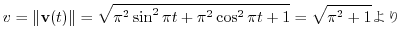 を
を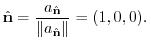 で割ってみましょう.
で割ってみましょう.
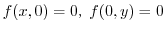
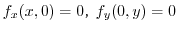
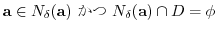
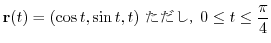 が整数のとき,
が整数のとき,
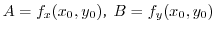
(1)
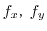 (2)
(2)
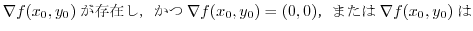 (3)
(3)
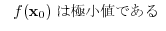 (4)
(4)
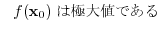
解
(1)
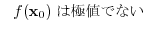 (2)
(2)
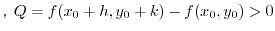 (3)
(3)
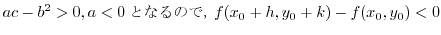
(4)
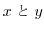

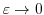 を満たす
を満たす を
を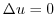 の
の 乗根ということを以前説明しました.これを記号で表そうとすると,
乗根ということを以前説明しました.これを記号で表そうとすると, が偶数か奇数かと
が偶数か奇数かと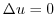 が正,零,負によって異なるので,簡単ではありません.そこで,一般に,
が正,零,負によって異なるので,簡単ではありません.そこで,一般に,
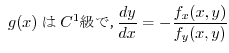 と表すときには,
と表すときには,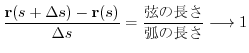 であるという条件をつけます.さて,
であるという条件をつけます.さて,
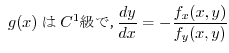 とはなんでしょうか.
とはなんでしょうか.
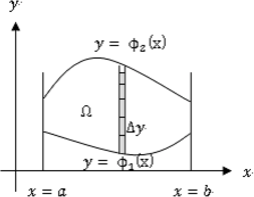 は
は
![$\sqrt[m]{a}$](img117.png) のことです.したがって,
のことです.したがって,
![$\displaystyle a^{\frac{n}{m}} = \sqrt[m]{a^{n}} = (\sqrt[m]{a})^{n}$](img118.png)
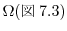 ,
,
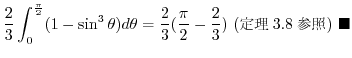 のとき,次の指数公式が成り立ちます.
のとき,次の指数公式が成り立ちます.
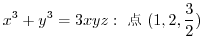
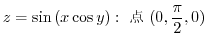
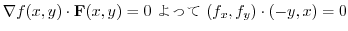
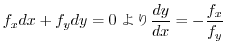
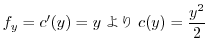
これをさらに有理数から実数へと拡張しようとするためには,極限値の話が必要となります.
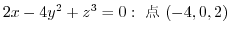 ,
, 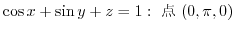 ,
,  のとき,次の値を求めよう.
のとき,次の値を求めよう.
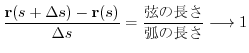 ,
,  を整数とするとき,次の式を簡単にしよう.
を整数とするとき,次の式を簡単にしよう.