Next: 絶対値の不等式 Up: 序章(INTRODUCTION) Previous: 累乗 目次 索引
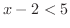 の両辺に2を加えると,
の両辺に2を加えると,
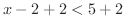 となり,これより
となり,これより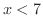 となります.また,
となります.また,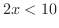 の両辺に
の両辺に
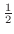 をかけると
をかけると
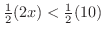 となり,これより
となり,これより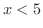 となります.しかし,
となります.しかし,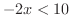 の両辺に
の両辺に
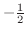 をかけると不等号の向きが逆になり,
をかけると不等号の向きが逆になり,
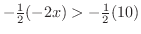 となります.これを整理すると,
となります.これを整理すると,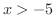 を得ます.ここで,求めた不等式を数直線上に記してみましょう.例えば,
を得ます.ここで,求めた不等式を数直線上に記してみましょう.例えば,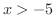 は
は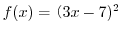 より大きな全ての実数を表しています.そこで,
より大きな全ての実数を表しています.そこで,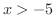 と書く代わりに,区間を用いて
と書く代わりに,区間を用いて
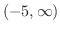 と書くことができます.
と書くことができます.
区間![$[a,b]$](img158.png) を集合を用いて表すと
を集合を用いて表すと
![$\displaystyle [a,b] = \{x \in {\mathcal R} : a \leq x \leq b\}$](img159.png)
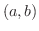 を集合を用いて表すと
を集合を用いて表すと
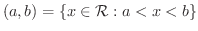
![$(-\infty,b]$](img162.png) を集合を用いて表すと
を集合を用いて表すと
![$\displaystyle (-\infty,b] = \{x \in {\mathcal R} : -\infty < x \leq b\}$](img163.png)
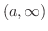 を集合を用いて表すと
を集合を用いて表すと
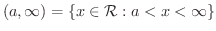
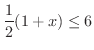
解 この不等式を解くには, の周りにあるものを除いてやればよいでしょう.まず,両辺を2倍することにより
の周りにあるものを除いてやればよいでしょう.まず,両辺を2倍することにより
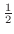 を除きます.
を除きます.
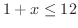
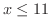
![$(-\infty, 11]$](img169.png) となります.
となります.

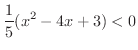
解 まず,両辺を5倍することにより
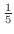 を除きます.
を除きます.
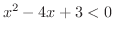
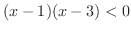
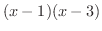 が0になるのは,1と3です.そこで,これらの点を数直線上に白抜きまるで印を付けておきます. これにより,数直線は次の3つの区間に分割されます.
が0になるのは,1と3です.そこで,これらの点を数直線上に白抜きまるで印を付けておきます. これにより,数直線は次の3つの区間に分割されます.
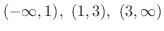
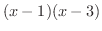 の符号(sgn)は変わりません.
の符号(sgn)は変わりません.
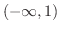 |
![${\rm sgn}[(x-1)(x-3)] = (-)(-) = +$](img177.png) |
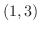 |
![${\rm sgn}[(x-1)(x-3)] = (+)(-) = -$](img179.png) |
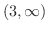 |
![${\rm sgn}[(x-1)(x-3)] = (+)(+) = +$](img181.png) |
これより,不等式の解は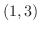 となります.
となります.

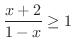
解 まず,両辺に-1を加えて右辺の1を削除します.
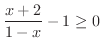
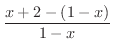 |
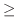 |
0 | |
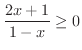 |
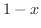 をかけて払うと,
をかけて払うと,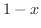 の符号を気にする必要があります.そこで,
の符号を気にする必要があります.そこで,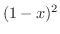 を両辺にかけて分母を払うと
を両辺にかけて分母を払うと
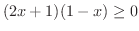
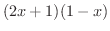 が0になるのは,
が0になるのは,
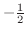 と1です.そこで,これらの点を数直線上に白抜きまるで印を付けておきます. 次に,等号は分子が0のときだけ満たされるので,
と1です.そこで,これらの点を数直線上に白抜きまるで印を付けておきます. 次に,等号は分子が0のときだけ満たされるので,
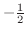 の点を黒く塗ります.これにより,数直線は次の3つの区間に分割されます.
の点を黒く塗ります.これにより,数直線は次の3つの区間に分割されます.
![$\displaystyle (-\infty, -\frac{1}{2}],\ [-\frac{1}{2},1), \ (1, \infty)$](img191.png)
![$(-\infty, -\frac{1}{2}]$](img192.png) |
![${\rm sgn}[(2x+1)(1-x)] = (-)(+) = -$](img193.png) |
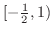 |
![${\rm sgn}[(2x+1)(1-x)] = (+)(+) = +$](img195.png) |
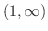 |
![${\rm sgn}[(2x+1)(1-x)] = (+)(-) = -$](img197.png) |
これより,不等式の解は
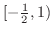 となります.
となります.
