Next: 関数(FUNCTIONS) Up: 序章(INTRODUCTION) Previous: 不等式 目次 索引
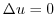 の絶対値は
の絶対値は
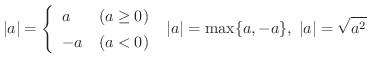
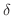 (デルタ)と
(デルタ)と
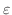 (イプシロン)を用います.
(イプシロン)を用います.
まず,不等式
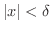
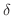 は正の数.
は正の数.
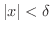 とは,
とは, が原点から
が原点から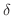 の範囲内にあるということです.つまり,
の範囲内にあるということです.つまり, は
は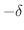 から
から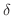 の間にあるということです.したがって,
の間にあるということです.したがって,
次に,
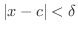 とは,
とは, が点
が点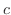 から
から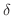 の範囲にあるということです.したがって,
の範囲にあるということです.したがって,
最後に,
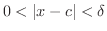 とは,
とは,
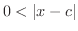 でかつ
でかつ
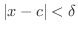 であるということです.最初の不等号は
であるということです.最初の不等号は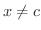 であるといっています.したがって,
であるといっています.したがって,
となります.
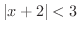
解 式(3)より,
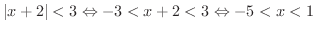
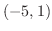

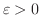 のとき,
のとき,
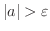 とは,原点から
とは,原点から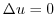 までの距離が
までの距離が
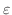 より大きいことを表している.したがって,
より大きいことを表している.したがって,
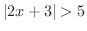
解 式(5)より,
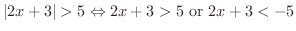
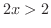 よって
よって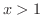 . また,2つ目の不等式から
. また,2つ目の不等式から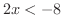 よって
よって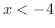 .したがって,不等式の解は
.したがって,不等式の解は
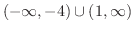

微分積分学の基本的な不等式の中に,三角不等式(triangle inequality)とよばれるものがあります.
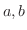 に対して
に対して
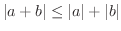
が成り立つ.
証明 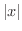 を
を
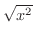 とおくと証明は簡単です.まず,
とおくと証明は簡単です.まず,
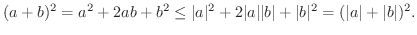
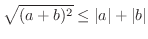
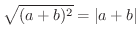

微分積分学で用いられる不等式には,次のものもあります.
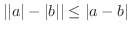
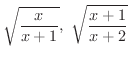
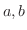 に対して,
に対して,