Next: 2重積分の応用(application of double integrals) Up: 重積分法(MULTIPLE INTEGRATION) Previous: 変数変換(change of variables) 目次 索引
これまでに扱った2重積分は,領域  が有界でかつ関数
が有界でかつ関数  も
も  上で有界のときでした.ここではもう少し広い範囲での2重積分,つまり
上で有界のときでした.ここではもう少し広い範囲での2重積分,つまり  が有界でない場合を考えてみましょう.
が有界でない場合を考えてみましょう.
 内の有界な閉領域の列
内の有界な閉領域の列
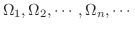 が
が
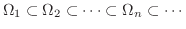
 内のどのような集合も必ずある
内のどのような集合も必ずある
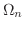 に含まれるようにでき,また,
に含まれるようにでき,また,  が各
が各
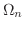 上で積分可能で
上で積分可能で
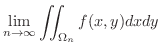
 は
は  上で積分可能(integrable) であるといい,次のように定義します.
上で積分可能(integrable) であるといい,次のように定義します.
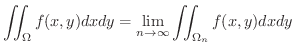
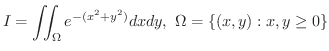
解
まず,領域  は有界でないので,次のような有界な閉領域の列
は有界でないので,次のような有界な閉領域の列
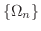 を考えます.
を考えます.
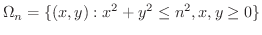
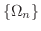 を図示すると図7.8を得ます.
を図示すると図7.8を得ます.
 上での積分は極座標変換
上での積分は極座標変換
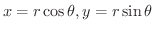 を用いて行うと,
を用いて行うと,
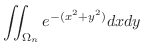 |
 |
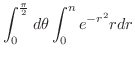 |
|
 |
![$\displaystyle \frac{\pi}{2}\left[-\frac{e^{-r^2}}{2}\right ]_{0}^{n} = \frac{\pi}{4}(1 - e^{-n^2})$](img4007.png) |
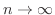 とすると
とすると 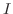 が求まり,
が求まり, 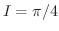 .
.

次に  上で
上で  が有界でない場合を考えてみましょう.
が有界でない場合を考えてみましょう.
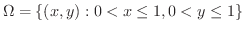 のとき,次の2重積分を求めてみましょう.
のとき,次の2重積分を求めてみましょう.
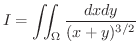
解
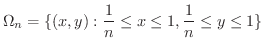
これより,
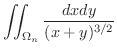 |
 |
![$\displaystyle \int_{1/n}^{1}dx\int_{1/n}^{1} \frac{dy}{(x+y)^{3/2}} = \int_{1/n}^{1}\left[-\frac{2}{(x+y)^{1/2}}\right ]_{\frac{1}{n}}^{1}dx$](img4014.png) |
|
 |
![$\displaystyle 2\int_{1/n}^{1}[(x+\frac{1}{n})^{-\frac{1}{2}} - (x+1)^{-\frac{1}{2}} ]dx$](img4015.png) |
||
 |
![$\displaystyle 2\left[2(x+\frac{1}{n})^{\frac{1}{2}} - 2(x+1)^{\frac{1}{2}}\right ]_{\frac{1}{n}}^{1}$](img4016.png) |
||
 |
![$\displaystyle 4[2(1+\frac{1}{n})^{\frac{1}{2}} - \sqrt{2} - (\frac{2}{n})^{\frac{1}{2}}]$](img4017.png) |
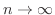 とすると
とすると 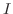 が求まります.
が求まります.
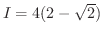 .
.
