Next: 3重積分(triple integrals) Up: 重積分法(MULTIPLE INTEGRATION) Previous: 広義積分(improper integrals) 目次 索引
ここでは2重積分の応用としてまず面積を考えます.図7.10のような有界閉領域  の面積は
の面積は
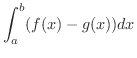
で与えられますが,
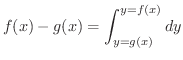
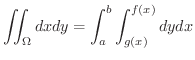
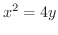 と直線
と直線
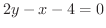 で囲まれた領域
で囲まれた領域  の面積を求めてみましょう.
の面積を求めてみましょう.
解
図7.11よりV-simpleを用いると
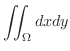 |
 |
![$\displaystyle \int_{-2}^{4}dx\int_{\frac{x^2}{4}}^{\frac{x+4}{2}}dy
= \int_{-2}^{4}[\frac{x+4}{2} - \frac{x^2}{4}]dx$](img4037.png) |
|
 |
![$\displaystyle \left[\frac{x^2}{4} +2x - \frac{x^3}{12}\right ]_{-2}^{4} = \frac{16 - 4}{4} + 2(4+2) -\frac{1}{12}(64 + 8)$](img4038.png) |
||
 |
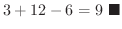 |
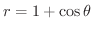 の内側で
の内側で 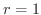 の外側の領域
の外側の領域  の面積を求めてみましょう.
の面積を求めてみましょう.
解
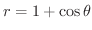 と
と 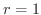 の交点を求めると,
の交点を求めると,
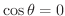 より
より
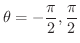 .よって,変数変換
.よって,変数変換
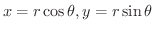 を行なうと,領域
を行なうと,領域  は領域
は領域
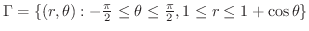 に移されます.図7.12参照.よって
に移されます.図7.12参照.よって
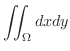 |
 |
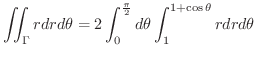 |
|
 |
![$\displaystyle 2\int_{0}^{\frac{\pi}{2}} \left[\frac{r^2}{2}\right ]_{1}^{1+\cos...
...ta = 2\int_{0}^{\frac{\pi}{2}}\frac{2\cos{\theta} + \cos^{2}{\theta}}{2}d\theta$](img4046.png) |
||
 |
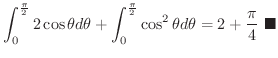 |
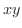 平面上の有界閉領域
平面上の有界閉領域  上で定義された関数
上で定義された関数
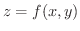 が
が 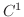 級であるとき,
級であるとき,
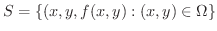
 の曲面積
の曲面積 を求めてみましょう.
を求めてみましょう.
図7.13 で四辺形PQRSにおいてベクトル
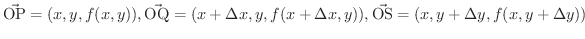
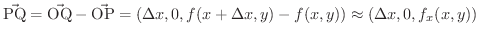
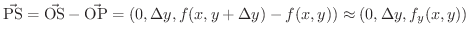
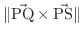 で近似されます.ここで,
で近似されます.ここで,
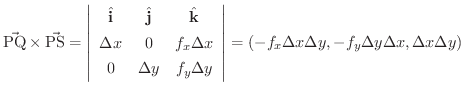
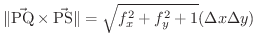
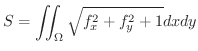
 は曲面
は曲面  の
の 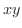 平面への正射影です.
平面への正射影です.
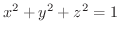 が円柱面
が円柱面
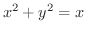 によって切り取られる部分の曲面積
によって切り取られる部分の曲面積 を求めてみましょう.
を求めてみましょう.
解
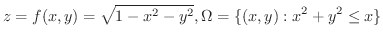
 |
 |
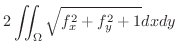 |
|
 |
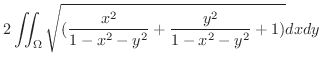 |
||
 |
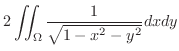 |
 は
は
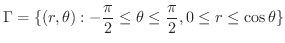
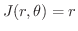 より
より
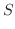 |
 |
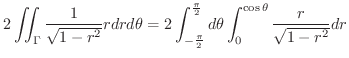 |
|
 |
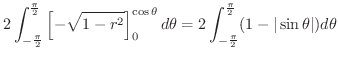 |
||
 |
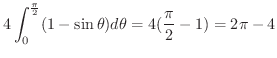 |

有界閉領域  と
と  上の連続関数
上の連続関数
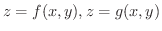 があり,
があり,  上で
上で
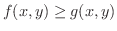 とします.このとき
とします.このとき  の境界
の境界
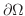 を通り
を通り 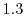 軸に平行な直線群と
軸に平行な直線群と 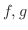 のグラフ曲面で囲まれた立体の体積は
のグラフ曲面で囲まれた立体の体積は
![$\displaystyle V = \iint_{\Omega}[f(x,y) - g(x,y)]dxdy $](img4073.png)
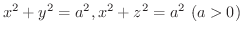 によって囲まれた立体の体積を求めてみましょう.
によって囲まれた立体の体積を求めてみましょう.
解
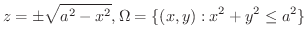
 軸に対して対称.したがって
軸に対して対称.したがって
 |
 |
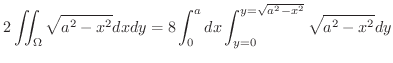 |
|
 |
![$\displaystyle 8\int_{0}^{a}(a^2 - x^2)dx = 8\left[a^2 x - \frac{x^3}{3}\right ]_{0}^{a} = \frac{16a^3}{3}
\ensuremath{\ \blacksquare}$](img4079.png) |
(a) 曲線
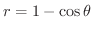 で囲む部分
で囲む部分
(b)
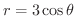 の内側で
の内側で
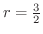 の外側の部分
の外側の部分
(c)
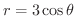 の内側で
の内側で
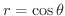 の外側の部分
の外側の部分
(a)
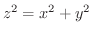 の
の
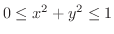 ,
, 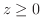 の部分
の部分
(b) 平面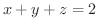 の
の
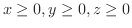 の部分
の部分
(c) 双曲方物面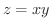 の円柱面
の円柱面
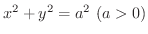 の内部にある部分
の内部にある部分
(a) 放物面
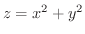 と平面
と平面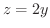 によって囲まれた部分
によって囲まれた部分
(b) 放物面
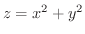 と円柱
と円柱
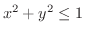 によって囲まれる部分
によって囲まれる部分
(a) 曲線
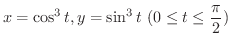 と両軸とで囲む部分
と両軸とで囲む部分
(b)
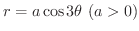 の囲む部分
の囲む部分
(c) 曲線
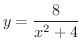 と
と
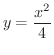 で囲む部分
で囲む部分
(a) 半径  の球面
の球面
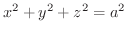
(b) 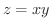 の
の
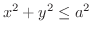 に対応する部分
に対応する部分
(c) 円柱
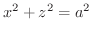 が円柱
が円柱
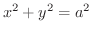 によって切り取られる部分
によって切り取られる部分
(d)
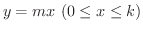 を
を  軸の回りに回転してできる曲面
軸の回りに回転してできる曲面 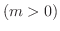
(a) 円柱
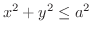 の
の
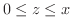 の部分
の部分
(b)
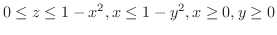 で定まる閉領域
で定まる閉領域
(c) 球
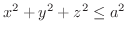 と円柱
と円柱
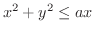 の共通部分
の共通部分
(d) 円錐面
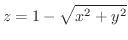 と平面
と平面 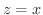 および
および 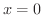 で囲まれる部分
で囲まれる部分