Next: ベクトル解析(VECTOR ANALYSIS) Up: 重積分法(MULTIPLE INTEGRATION) Previous: 2重積分の応用(application of double integrals) 目次 索引
2重積分と同様に3重積分も累次積分として表わすことができます.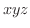 空間の有界閉領域を
空間の有界閉領域を 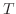 とし,
とし, 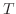 の
の 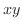 平面への正射影を
平面への正射影を
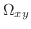 とすると,
とすると, 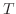 は
は
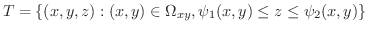
![$\displaystyle \iiint_{T}f(x,y,z)dxdydz = \iint_{\Omega_{xy}}[\int_{\psi_{1}(x,y)}^{\psi_{2}(x,y)}f(x,y,z)dz]dxdy $](img4111.png)
が成り立ちます.さらに,
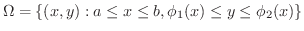
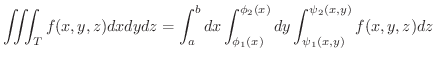
が成り立ちます.
3重積分についても2重積分の場合と同様に次の定理が成り立ちます.
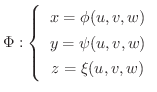 によって,
によって, 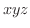 空間の有界な閉領域
空間の有界な閉領域 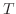 と
と 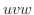 空間の有界な閉領域
空間の有界な閉領域
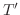 が1対1に対応し,
が1対1に対応し,
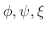 が
が 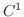 級で
級で
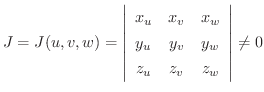
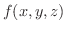 が
が 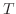 上で連続ならば,
上で連続ならば,
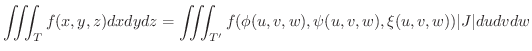
ここで変数変換の中で特によく用いられる円柱座標変換と球面座標変換について学びます.
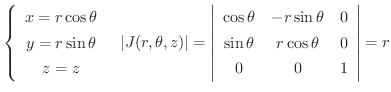
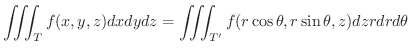
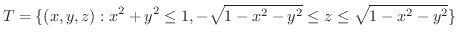 のとき.次の値を求めてみましょう.
のとき.次の値を求めてみましょう.
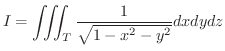
解
円柱座標変換を用いると, 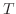 は
は
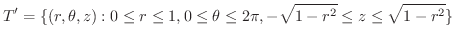
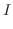 |
 |
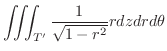 |
|
 |
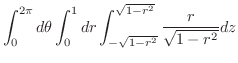 |
||
 |
![$\displaystyle \int_{0}^{2\pi} \int_{0}^{1} 2r dr = 2\pi \cdot \left[r^{2} \right ]_{0}^{1} = 2\pi \ \ensuremath{\ \blacksquare}$](img4127.png) |
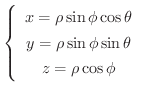
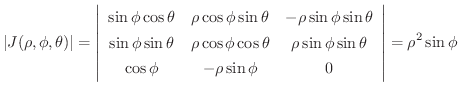
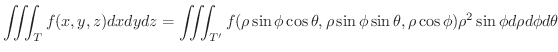
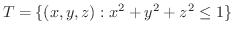 のとき,次の値を求めてみましょう.
のとき,次の値を求めてみましょう.
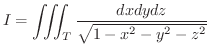
解
球面座標変換を用いると,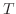 は
は
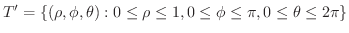
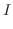 |
 |
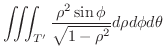 |
|
 |
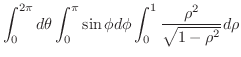 |
||
 |
![$\displaystyle 2\pi \cdot 2 \cdot \left[\frac{1}{2}\left(- \rho \sqrt{1 - \rho^2} + \sin^{-1}{\rho} \right) \right ]_{0}^{1}$](img4137.png) |
||
 |
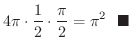 |
2重積分の応用で 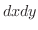 を面積として考えました.同じようにして,ここでは,
を面積として考えました.同じようにして,ここでは, 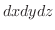 を体積として考えることができます.
を体積として考えることができます.
もし密度 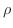 がそれぞれの点で連続的に変化し,
がそれぞれの点で連続的に変化し,
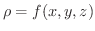 ならば,立体
ならば,立体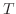 の質量
の質量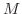 は
は
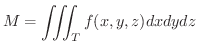
で表わせます.特に密度
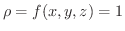 のとき
のとき
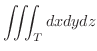
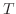 の体積と考えることができます.
の体積と考えることができます.
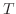 の体積を求めてみましょう.
の体積を求めてみましょう.
解
3重積分を計算するために 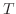 を適当な座標軸面に正射影します.ここでは
を適当な座標軸面に正射影します.ここでは 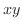 平面に正射影します.ここでV-simpleを用いると
平面に正射影します.ここでV-simpleを用いると
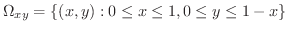
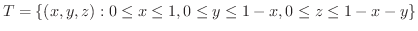
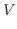 |
 |
![$\displaystyle \iint_{\Omega_{xy}}[\int_{0}^{1-x-y}dz]dxdy = \int_{0}^{1}\int_{0}^{1-x}(1-x-y)dydx$](img4149.png) |
|
 |
![$\displaystyle \int_{0}^{1} \left[(1-x)y - \frac{y^2}{2}\right ]_{0}^{1-x} dx = \int_{0}^{1}\frac{(1-x)^{2}}{2}dx$](img4150.png) |
||
 |
![$\displaystyle - \left[\frac{(1-x)^{3}}{6}\right ]_{0}^{1} = \frac{1}{6}$](img4151.png) |

実際,体積を求めるのが目的ならば,底面積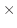 高さ
高さ
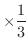 よりすぐに求まります.そこで,ここでは,三角錐の各点における密度が異なる場合を考えてみます.
よりすぐに求まります.そこで,ここでは,三角錐の各点における密度が異なる場合を考えてみます.
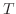 の密度が
の密度が
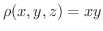 のときの質量を求めてみましょう.
のときの質量を求めてみましょう.
解
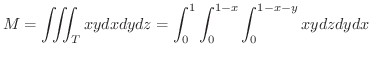
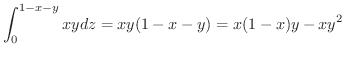
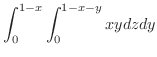 |
 |
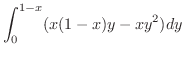 |
|
 |
![$\displaystyle \left[\frac{1}{2}x(1-x)y^2 - \frac{1}{3}xy^3\right ]_{0}^{1-x} = \frac{1}{6}x(1-x)^{3}$](img4159.png) |
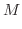 |
 |
 |
|
 |
![$\displaystyle \frac{1}{6}\left[\frac{1}{2}x^2 - x^3 + \frac{3}{4}x^4 -\frac{1}{5}x^5\right ]_{0}^{1} = \frac{1}{120}
\ensuremath{\ \blacksquare}$](img4162.png) |
体積,質量と求めてきたので最後に重心を求めてみましょう.まず平面上に  個の点
個の点
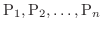 からなる質点系があって,点
からなる質点系があって,点
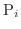 の座標は
の座標は
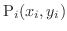 .また
.また
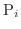 の質量が
の質量が 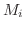 で与えられているとします.このときこれらの点がつりあうように
で与えられているとします.このときこれらの点がつりあうように  軸に垂直な線
軸に垂直な線
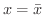 を引くと,この線に対して反時計回りのモーメントと時計回りのモーメントはつりあっているはずです.よって
を引くと,この線に対して反時計回りのモーメントと時計回りのモーメントはつりあっているはずです.よって
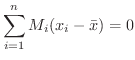
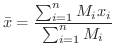
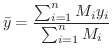
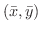 を 質点系の重心(centroid) といいます.
を 質点系の重心(centroid) といいます.
平面上の有界閉領域  の各点
の各点
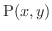 に密度
に密度 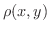 が与えられているときは,
が与えられているときは,  の分割
の分割
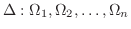 をとり,それぞれの
をとり,それぞれの
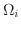 の中から任意に点
の中から任意に点
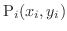 を選び,質点系
を選び,質点系
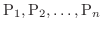 の重心
の重心
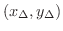 を考えます.
を考えます.
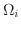 の面積を
の面積を
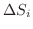 とおくと
とおくと
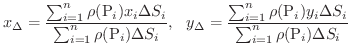
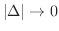 とすると
とすると
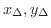 はそれぞれ次の
はそれぞれ次の
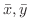 に収束します.
に収束します.
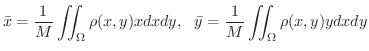
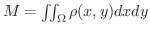 で質量(mass)を表わします.
で質量(mass)を表わします.
空間の閉領域 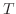 に,密度
に,密度
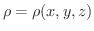 が与えられている場合にも,同様にして重心
が与えられている場合にも,同様にして重心
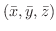 が次のように定まります.
が次のように定まります.
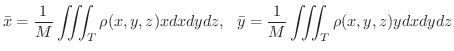
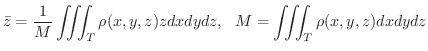
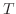 の重心を求めてみましょう.
の重心を求めてみましょう.
解
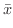 |
 |
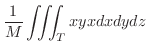 |
|
 |
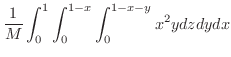 |
||
 |
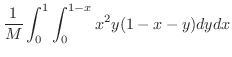 |
||
 |
![$\displaystyle \frac{1}{M}\int_{0}^{1}\left[(\frac{x^{2}(1-x)y^{2}}{2} - \frac{x^{2}y^{3}}{3})\right ]_{0}^{1-x}dx$](img4190.png) |
||
 |
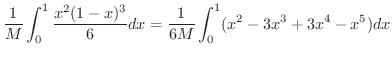 |
||
 |
![$\displaystyle \frac{1}{6M}\left[\frac{x^{3}}{3} - \frac{3x^{4}}{4} + \frac{3x^{5}}{5} - \frac{x^{6}}{6} \right ]_{0}^{1} = \frac{1}{360M}$](img4192.png) |
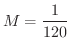 より
より
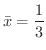 .残りの
.残りの
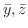 は各自求めて下さい.
は各自求めて下さい.

(a) ボール
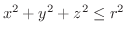 の質量.ただし,密度は中心からの距離に比例するとする.
の質量.ただし,密度は中心からの距離に比例するとする.
(b) 平面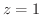 と曲面
と曲面
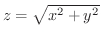 で囲まれた円錐の質量.ただし,密度は原点からの距離に比例するとする.
で囲まれた円錐の質量.ただし,密度は原点からの距離に比例するとする.
(c) 放物面
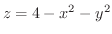 と曲面
と曲面
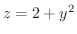 で囲まれた部分の体積.
で囲まれた部分の体積.
(a) 密度一定のとき, 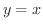 と
と
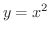 とで囲まれた閉領域
とで囲まれた閉領域
(b) 密度一定のとき,
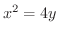 と
と
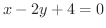 とで囲まれた閉領域
とで囲まれた閉領域
(c) 密度一定のとき,
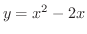 と
と
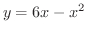 とで囲まれた閉領域
とで囲まれた閉領域
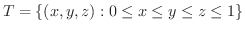 のとき,次の3重積分を求めよう.
のとき,次の3重積分を求めよう.
(a) 密度一定のとき, 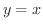 と
と
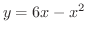 とで囲まれた閉領域
とで囲まれた閉領域
(b) 密度が中心からの距離に比例するときの,半球
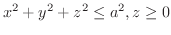
(c) 密度一定のとき,底面の半径が 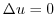 ,高さが
,高さが 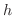 の直円錐.
の直円錐.
(d) 密度一定のとき,
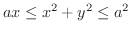 であらわせる領域
であらわせる領域
(f) 密度が原点からの距離に比例するときの,
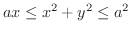 であらわせる領域
であらわせる領域