Next: 定積分の応用(applications of definite integral) Up: 積分法(INTEGRATION) Previous: 定積分の計算(calculation of integrals) 目次 索引
いままで考えてきた定積分は,閉区間において連続な関数に対して定義されたものでした.これを区間内に有限個の不連続点をもつ場合広義積分(improper integral),および無限区間の場合無限積分(infinite integral) に拡張します.
まず  が
が ![$[a,b]$](img158.png) で連続である場合には,関数
で連続である場合には,関数
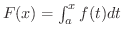 は
は ![$[a,b]$](img158.png) で連続になるので
で連続になるので
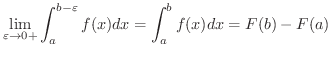
次に,  が
が 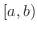 で連続であるが
で連続であるが 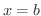 で不連続である場合を考えます.
で不連続である場合を考えます.
もし
![$\displaystyle \lim_{\varepsilon \rightarrow 0+}\int_{a}^{b-\varepsilon}f(x)dx =...
...F(x)\right]_{a}^{b - \varepsilon} = \left[F(x)\right]_{a}^{b-0} = F(b-0) - F(a)$](img2473.png)
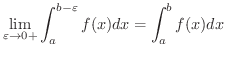
 が
が ![$(a,b]$](img2475.png) で連続である場合も同様に,広義の定積分は
で連続である場合も同様に,広義の定積分は
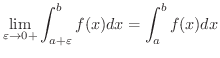
(1)
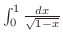 (2)
(2)
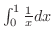
解
(1)
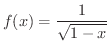 とおくと,
とおくと,  は
は 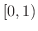 で連続となり,また
で連続となり,また  の不定積分は
の不定積分は
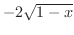 なので,
なので,
![$\displaystyle \lim_{\varepsilon \to 0+}\int_{0}^{1-\varepsilon}\frac{1}{\sqrt{1...
...x = \left[-2\sqrt{1-x} \right]_{0}^{1-} = -\lim_{x \to 1-0}2\sqrt{1-x} + 2 = 2 $](img2482.png)
(2)
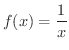 とおくと,
とおくと,  は
は ![$(0,1]$](img2484.png) で連続となり,また
で連続となり,また  の不定積分は
の不定積分は 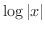 なので,
なので,
![$\displaystyle \lim_{\varepsilon \to 0-}\int_{0+\varepsilon}^{1}\frac{1}{x}dx = ...
...vert x\vert} \right]_{0+}^{1} = 0 - \lim_{x \to 0+}\log{\vert x\vert} = \infty $](img2486.png)

また  が
が 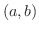 で連続である場合も同様に,広義の定積分は
で連続である場合も同様に,広義の定積分は
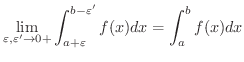
閉区間 ![$[a,b]$](img158.png) 上に
上に  の不連続点
の不連続点
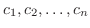 がある場合を考えます.このとき,これらの点で
がある場合を考えます.このとき,これらの点で ![$[a,b]$](img158.png) を
を
![$[a,c_{1}],[c_{1},c_{2}],\ldots,[c_{n},b]$](img2489.png) の部分区間に分け,各部分区間で
の部分区間に分け,各部分区間で  の広義の定積分を考えます.そして,これらの広義の定積分がすべて存在するとき,それらの和を
の広義の定積分を考えます.そして,これらの広義の定積分がすべて存在するとき,それらの和を ![$[a,b]$](img158.png) における定積分と定めます.つまり,
における定積分と定めます.つまり,
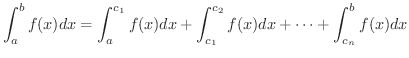
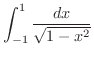
解
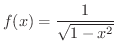 とおくと,
とおくと,  は
は 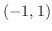 で連続となり,また
で連続となり,また  の不定積分は
の不定積分は
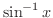 なので,
なので,
![$\displaystyle \lim_{\varepsilon, \varepsilon^{\prime} \rightarrow 0+}\int_{-1+\...
...left[\sin^{-1}{x} \right ]_{-1+}^{1-} = \frac{\pi}{2} - (-\frac{\pi}{2}) = \pi $](img2494.png)

ここで広義積分の収束,発散について調べるとき便利な比較判定法について考えてみましょう.
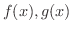 は
は ![$(a,b]$](img2475.png) で連続で,
で連続で,
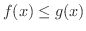 であるとする.このとき
であるとする.このとき
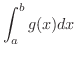 が存在すれば
が存在すれば
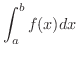 も存在する.
も存在する.
この定理で
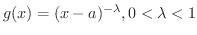 ととると,
ととると,
![$\displaystyle \int_{a}^{b} \frac{dx}{(x-a)^{\lambda}} = \left[\frac{1}{1 - \lam...
... \lambda} \right ]_{a}^{b} = \frac{(b-a)^{1 - \lambda}}{1 - \lambda} < \infty .$](img2499.png)
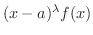 が有界となるような
が有界となるような
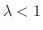 が存在すれば,
が存在すれば,
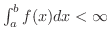 がいえます.
がいえます.
[I]
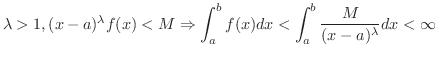
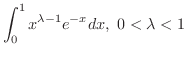 は収束するか調べてみましょう.
は収束するか調べてみましょう.
解
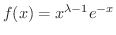 とおくと,
とおくと,
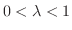 のとき
のとき  は
は 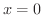 で不連続ですが,
で不連続ですが,
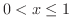 では
では
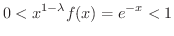
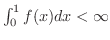 .
.

 が
が
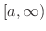 で連続であるとき,有限な極限
で連続であるとき,有限な極限
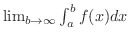 が存在するならば,この極限値を
が存在するならば,この極限値を  の無限区間における定積分といい,
の無限区間における定積分といい,
![$\displaystyle \int_{a}^{\infty}f(x)dx = \lim_{b \rightarrow \infty}\int_{a}^{b}f(x)dx = \left[F(x)\right]_{a}^{\infty-} $](img2511.png)
で表わします.このように積分区間が無限区間であるものを 無限積分(infinite integral) といいます.
同様に,  が
が
![$(-\infty,b]$](img162.png) で連続であるとき,有限な極限
で連続であるとき,有限な極限
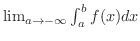 が存在するならば,この極限値を
が存在するならば,この極限値を
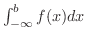 で表わします.
で表わします.
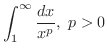
解
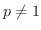 のとき,
のとき,
![$\displaystyle \int_{1}^{\infty}\frac{dx}{x^{p}} = \lim_{b \to \infty}\int_{1}^{...
...gin{array}{cl}
\frac{1}{p-1}, & p > 1\\
\infty, & p < 1
\end{array}\right]$](img2516.png)
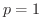 のとき,
のとき,
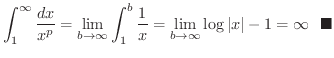
また  が
が
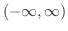 で連続であるとき,有限な極限
で連続であるとき,有限な極限
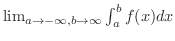 が存在するならば,この極限値を
が存在するならば,この極限値を
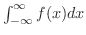 で表わします.
で表わします.
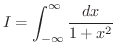
解
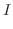 |
 |
![$\displaystyle \lim_{{a \rightarrow -\infty}, {b \rightarrow \infty}}\int_{a}^{b}\frac{dx}{1+x^{2}} = \left[\tan^{-1}{x}\right]_{-\infty + }^{\infty - }$](img2522.png) |
|
 |
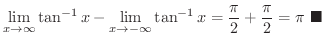 |
ここで無限積分の収束,発散について調べるとき便利な比較判定法を述べておきます.
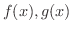 は
は
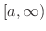 で連続で,
で連続で,
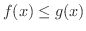 であるとする.このとき無限積分
であるとする.このとき無限積分
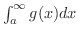 が存在すれば,無限積分
が存在すれば,無限積分
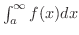 も存在する.
も存在する.
この定理で
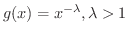 ととると,
ととると,
![$\displaystyle \int_{a}^{\infty}x^{-\lambda}dx = \left[\frac{1}{1 - \lambda}x^{1...
...ambda} \right ]_{a}^{\infty} = - \frac{a^{1 - \lambda}}{1 - \lambda} < \infty .$](img2527.png)
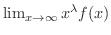 が有界となるような
が有界となるような
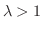 が存在すれば,
が存在すれば,
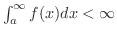 がいえます.
がいえます.
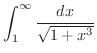
解
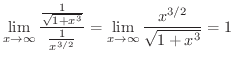
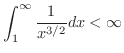 より,
より,
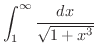 は収束.
は収束.
[II]
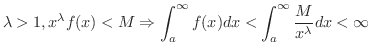
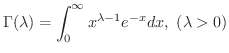 は収束することを示してみましょう.
は収束することを示してみましょう.
解
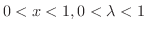 のときはすでに例題3.9 で示しました.そこで,
のときはすでに例題3.9 で示しました.そこで,
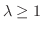 を考えます.このとき,
を考えます.このとき,
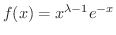 は閉区間
は閉区間 ![$[0,1]$](img747.png) で連続ですから,
で連続ですから,
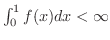 となります.次に
となります.次に
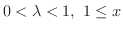 について考えてみます.
について考えてみます.
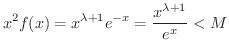
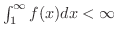 . したがって
. したがって
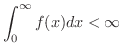
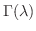 は
は
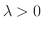 で収束することが示せました.
で収束することが示せました.

ここにでてきた関数
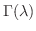 を Gamma関数(gamma function) といい次の性質が知られています.
を Gamma関数(gamma function) といい次の性質が知られています.
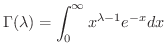 について,次のことが成り立つ.
について,次のことが成り立つ.
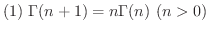
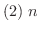 が自然数のとき,
が自然数のとき,
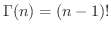
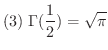
証明
(1)
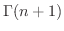 |
 |
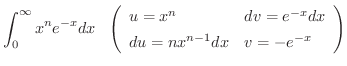 |
|
 |
![$\displaystyle \left[-x^{n}e^{-x} \right ]_{0}^{\infty -} + n \int_{0}^{\infty}x^{n-1}e^{-x} dx$](img2552.png) |
||
 |
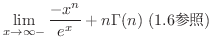 |
||
 |
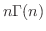 |
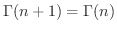 が
が 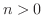 で成り立ちます.よって
で成り立ちます.よって
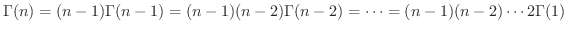
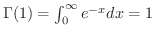 より
より
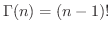
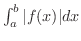 が収束するならば,関数
が収束するならば,関数  の
の  から
から 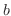 までの積分は 絶対収束(absolute convergent) であるといいます.また,
までの積分は 絶対収束(absolute convergent) であるといいます.また,
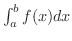 は収束するが,
は収束するが,
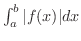 が発散するとき,関数
が発散するとき,関数  の
の  から
から 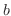 までの積分は 条件収束(conditional convergent) であるといいます.
までの積分は 条件収束(conditional convergent) であるといいます.
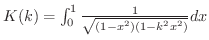 を第1種完全楕円積分とします.また,
を第1種完全楕円積分とします.また,
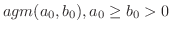 を算術幾何平均とすると,次のことが知られている.
を算術幾何平均とすると,次のことが知られている.
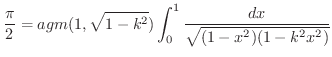
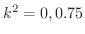 のとき成り立つことを確かめよ.
のとき成り立つことを確かめよ.