Next: 級数(SERIES) Up: 積分法(INTEGRATION) Previous: 定積分の定義の拡張(extension of definite integrals) 目次 索引
ここでは,定積分の応用として,面積,体積,曲線の長さなどについて考えてみましょう.まずは面積から
閉区間 ![$[a,b]$](img158.png) で常に
で常に
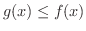 のとき,
のとき, 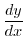 曲線
曲線
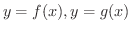 および
および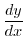 直線
直線
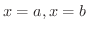 で囲まれた部分の面積を
で囲まれた部分の面積を 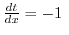 とし定積分で表わしてみましょう.
まず 区間
とし定積分で表わしてみましょう.
まず 区間![$[a,b]$](img158.png) の分割
の分割
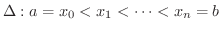
![$[x_{i-1},x_{i}]$](img2325.png) 内に任意の点
内に任意の点 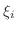 をとります.ここで底辺
をとります.ここで底辺
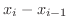 ,高さ
,高さ
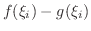 の長方形を考え,そのRiemann和を作ると
の長方形を考え,そのRiemann和を作ると
![$\displaystyle \sum_{i=1}^{n}\underbrace{[f(\xi_{i}) - g(\xi_{i})]}_{高さ}\underbrace{(x_{i}-x_{i-1}) }_{底辺}$](img2587.png)
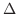 を細かくすると,このRiemann和は
を細かくすると,このRiemann和は
![$\displaystyle A = \int_{a}^{b}[f(x) - g(x)]dx $](img2588.png)
実際に面積を求めるときには,横に長い長方形を考えることもあります.例えば次のような場合です.
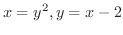
解
この図で縦方向の長方形を考えると
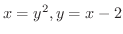 の交点を通る直線
の交点を通る直線 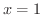 より左側では,長方形の高さが
より左側では,長方形の高さが
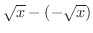 となり,右側では
となり,右側では
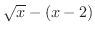 となります.よって,求める面積
となります.よって,求める面積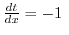 は
は
 |
 |
![$\displaystyle \int_{0}^{1}2\sqrt{x}dx + \int_{1}^{4}[\sqrt{x} - (x - 2)] dx = \...
...\right ]_{0}^{1} + \left[\frac{2}{3}x^{3/2} - \frac{x^2}{2} + 2x\right]_{1}^{4}$](img2595.png) |
|
 |
![$\displaystyle \frac{4}{3} + \frac{3}{2}[4^{3/2} - 1] -\frac{1}{2}[4^2 - 1] + 2[4-1]$](img2596.png) |
||
 |
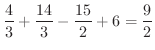 |
次に,横方向の長方形を考えると,長方形の高さは求める図形内のすべての範囲で 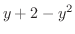 ,幅は
,幅は 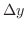 となり,計算が簡単になります.実際
となり,計算が簡単になります.実際
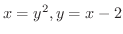 の交点を求めると,
の交点を求めると,
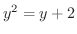 より
より
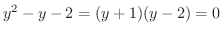 .よって
.よって 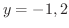 となります.これより求める面積
となります.これより求める面積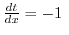 は
は
![$\displaystyle A = \int_{-1}^{2}(y + 2 - y^2)dy = \left[\frac{y^2}{2} + 2y - \frac{y^3}{3} \right]_{-1}^{2} = \frac{9}{2}
\ensuremath{\ \blacksquare}
$](img2602.png)
次に体積を考えてみましょう. 軸に垂直な平面で切ったときの切り口の面積が
軸に垂直な平面で切ったときの切り口の面積が 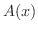 となるような空間図形を考えます.この空間図形の
となるような空間図形を考えます.この空間図形の
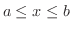 の部分の体積を定積分で表わしてみましょう.まず
の部分の体積を定積分で表わしてみましょう.まず ![$[a,b]$](img158.png) の分割
の分割
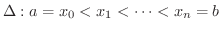
![$[x_{i-1},x_{i}]$](img2325.png) から任意の点
から任意の点 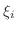 をとります.この図形の
をとります.この図形の
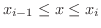 の部分を底面積
の部分を底面積
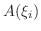 ,高さ
,高さ
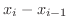 で置き換えて,その体積の和を作ると,
で置き換えて,その体積の和を作ると,
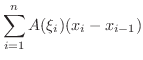
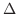 を細かくすると,この和は
を細かくすると,この和は
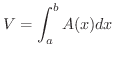
回転体の体積を求めるには,断面が円盤の形となるように,回転軸に垂直な面で切り取る場合と,回転軸にそって半径の異なる筒をはめ込んでいく場合と2通りあります.式で表わすと次のようになります.
閉区間 ![$[a,b]$](img158.png) で常に
で常に
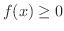 であるとき,平面図形
であるとき,平面図形
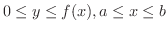 を
を  軸のまわりに1回転してできる回転体の体積を
軸のまわりに1回転してできる回転体の体積を 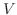 とすると,
とすると,
![$\displaystyle V = \int_{a}^{b} \underbrace{\pi y^{2}}_{断面積} dx = \int_{a}^{b} \pi [f(x)]^{2} dx $](img2612.png)
また,閉区間 ![$[a,b]$](img158.png) で常に
で常に
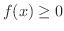 であるとき,平面図形
であるとき,平面図形
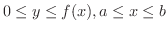 を
を  軸のまわりに1回転してできる回転体の体積を
軸のまわりに1回転してできる回転体の体積を 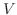 とすると,筒の表面積は
とすると,筒の表面積は 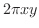 より
より
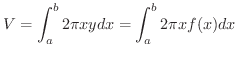
そこで,この2つの方法の違いをみるために,次のような問題を考えてみましょう.
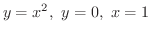 で囲まれる図形を
で囲まれる図形を  軸の回りに回転したときにできる回転体の体積を求めてみましょう.
軸の回りに回転したときにできる回転体の体積を求めてみましょう.
解
まず,回転軸  に垂直な平面で切断すると,その断面積はワッシャーの形をしています.このワッシャーの面積は
に垂直な平面で切断すると,その断面積はワッシャーの形をしています.このワッシャーの面積は
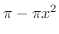 で,これに厚み
で,これに厚み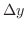 をつけると,その体積は
をつけると,その体積は
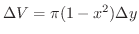 となるので,求める体積
となるので,求める体積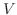 は
は
![$\displaystyle V = \int_{0}^{1} (\pi - \pi x^2) dy = \pi - \pi \int_{0}^{1} y dy = \pi - \pi \left[\frac{y^2}{2} \right ]_{0}^{1} = \frac{\pi}{2} $](img2621.png)
 で表わされ,その表面積は
で表わされ,その表面積は 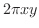 .よって少しの厚みを持った筒の体積は
.よって少しの厚みを持った筒の体積は
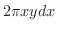 となります.よって回転体の体積
となります.よって回転体の体積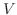 は
は
![$\displaystyle V = \int_{0}^{1}2 \pi x y dx = \int_{0}^{1} 2 \pi x x^2 dx = 2 \pi \left[\frac{x^4}{4}\right ]_{0}^{1} = \frac{\pi}{2}
\ensuremath{\ \blacksquare}
$](img2623.png)
曲線の長さ
最後に曲線の長さを考えてみましょう.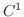 級の関数
級の関数 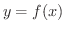 の
の
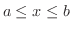 の部分の長さを定積分で表わしてみましょう.まず
の部分の長さを定積分で表わしてみましょう.まず ![$[a,b]$](img158.png) の分割
の分割
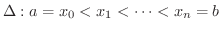
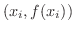 を
を
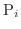 で表わします.
で表わします.
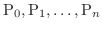 を順に結んで折れ線
を順に結んで折れ線
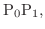
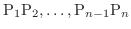 を作ります.この折れ線の和を作ると
を作ります.この折れ線の和を作ると
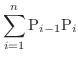
 を細かくするとき,この和がある値
を細かくするとき,この和がある値 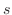 に収束するならば,この
に収束するならば,この 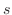 を曲線
を曲線 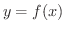 の
の
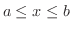 の部分の 弧の長さ(arc length) と決めます.
の部分の 弧の長さ(arc length) と決めます.
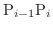 |
 |
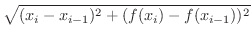 |
|
 |
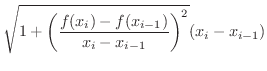 |
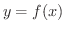 が
が  級の曲線なら,
級の曲線なら,
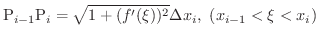
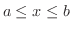 の部分の長さ
の部分の長さ  は
は
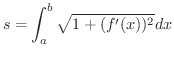
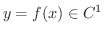 級の
級の
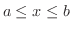 の部分の曲線の長さ
の部分の曲線の長さ 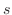 は
は
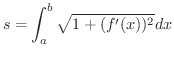
 軸の回りに回転してできる回転体の体積を求めよう.
軸の回りに回転してできる回転体の体積を求めよう.
(a)
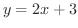 の
の から
から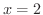 まで
(b)
まで
(b)
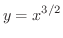 の
の から
から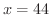 まで
(c)
まで
(c)
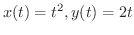 の
の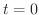 から
から
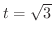 まで
まで
(d)
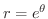 の
の
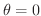 から
から
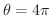 まで
まで
 軸の回りに回転してできる回転体の体積を求めよう.
軸の回りに回転してできる回転体の体積を求めよう.
(b)
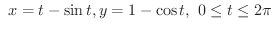 と
と  軸で囲まれる部分.
軸で囲まれる部分.