Next: 定積分の定義の拡張(extension of definite integrals) Up: 積分法(INTEGRATION) Previous: 定積分(definite integral) 目次 索引
不定積分の置換積分と部分積分についてすでに学んだので,ここでは定積分の置換積分と部分積分についての話から始めます.
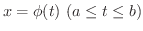 のとき次の式が成り立つ.
のとき次の式が成り立つ.
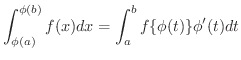
証明
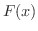 を
を  の原始関数とすると,
の原始関数とすると,
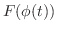 は
は
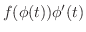 の原始関数である.したがって,微分積分学の基本定理より,
の原始関数である.したがって,微分積分学の基本定理より,
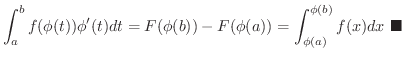
 について次の式が成り立つ.
について次の式が成り立つ.
![$\displaystyle \int_{a}^{b} udv = \left[uv\right]_{a}^{b} - \int_{a}^{b} vdu $](img2419.png)
証明
![$\int_{a}^{b}udv + \int_{a}^{b}vdu = \left[uv\right]_{a}^{b}$](img2420.png)

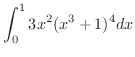
解
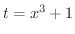 とおくと,
とおくと,
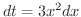 となるので,被積分関数は
となるので,被積分関数は 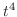 で表わすことができます.また積分範囲は
で表わすことができます.また積分範囲は
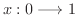 のとき,
のとき,
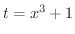 なので
なので
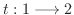 となります.よって
となります.よって
![$\displaystyle \int_{0}^{1}3x^{2}(x^{3}+1)^{4}dx = \int_{1}^{2}t^4 dt = \left[\f...
...\right ]_{1}^{2} = \frac{32 - 1}{5} = \frac{31}{5}
\ensuremath{\ \blacksquare}
$](img2427.png)
定積分でよく使われる積分に次のものがあります.
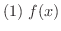 が偶関数ならば,
が偶関数ならば,
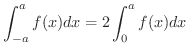
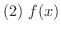 が奇関数ならば,
が奇関数ならば,
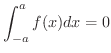
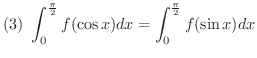
ただし,
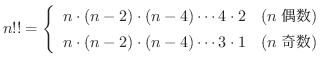
ここで,  が 偶関数(even function) とは
が 偶関数(even function) とは
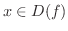 において,
において,
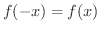 が成り立つことです.これを
が成り立つことです.これを  のグラフで考えるとy軸対称となります.また,
のグラフで考えるとy軸対称となります.また,  が 奇関数(odd function) とは
が 奇関数(odd function) とは
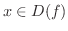 において,
において,
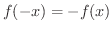 が成り立つことです.これを
が成り立つことです.これを  のグラフで考えると原点対称となります.
のグラフで考えると原点対称となります.
証明
(1)
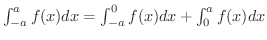 .と表わせるので,
.と表わせるので,
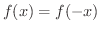 より
より
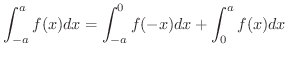
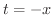 とおくと
とおくと 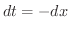 .また,
.また,
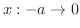 より
より
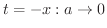 .よって
.よって
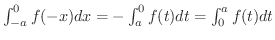 .これより,
.これより,
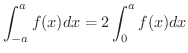
(2),(3)の証明は各自に任せます.
(4) 演習問題3.8-2より
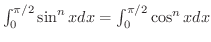 なので
なので
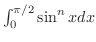 について証明しよう.
について証明しよう.
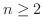 のときは,
のときは,
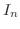 |
 |
![$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin^{n-1}{x}\sin{x}dx = -\left[\sin^{n-1...
...]_{0}^{\frac{\pi}{2}} + (n-1)\int_{0}^{\frac{\pi}{2}}\sin^{n-2}{x}\cos^{2}{x}dx$](img2447.png) |
|
 |
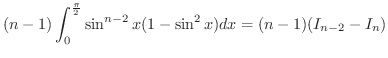 |
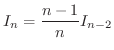
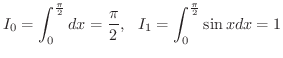
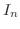 |
 |
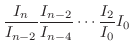 |
|
 |
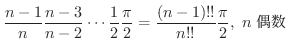 |
||
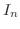 |
 |
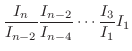 |
|
 |
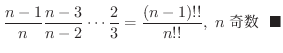 |
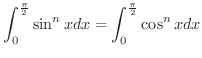 を示そう.
を示そう.
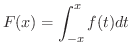 について以下のことについて答えよう.ただし,
について以下のことについて答えよう.ただし, は区間
は区間
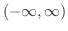 で微分可能な関数とする.
で微分可能な関数とする.
(a) 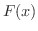 は奇関数であることを示そう.
は奇関数であることを示そう.
(b)  が偶関数ならば
が偶関数ならば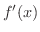 は奇関数であることを示そう.
は奇関数であることを示そう.
(c)
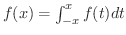 ならば
ならば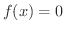 となることを示そう.
となることを示そう.
(d)  は偶関数と奇関数の和で表せることを示そう.
は偶関数と奇関数の和で表せることを示そう.