Next: 定積分の計算(calculation of integrals) Up: 積分法(INTEGRATION) Previous: 無理関数の積分法(integration of irrational functions) 目次 索引
ここではドイツの数学者 G.F.B. Riemann (1826-1917) によって示されたRiemann積分について学んでいきます.
 は閉区間
は閉区間 ![$[a,b]$](img158.png) で定義されているとします.この区間
で定義されているとします.この区間 ![$[a,b]$](img158.png) を次のような点
を次のような点
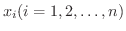 で
で  個の小区間に分割します.
個の小区間に分割します.
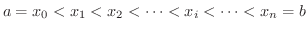
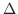 で表わし,
で表わし,
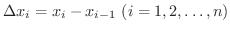 のうちで最も大きい値を
のうちで最も大きい値を 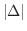 で表わします.いま,それぞれの小区間
で表わします.いま,それぞれの小区間
![$[x_{i-1},x_{i}]$](img2325.png) のなかに任意の点
のなかに任意の点 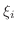 をとり,Riemann和(Riemann sum) とよばれる次の和を考えます.
をとり,Riemann和(Riemann sum) とよばれる次の和を考えます.
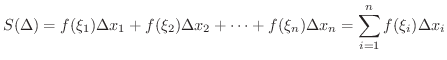
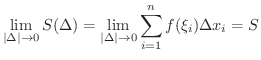
 が存在するならば,この
が存在するならば,この  を
を  の 定積分(definite integral) といい,
の 定積分(definite integral) といい,  は
は ![$[a,b]$](img158.png) で積分可能(integrable) であるといいます.また,この
で積分可能(integrable) であるといいます.また,この  を次のように表わします.
を次のように表わします.
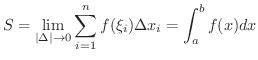
つまり関数  が
が ![$[a,b]$](img158.png) で積分可能であるということは,分割の仕方および点
で積分可能であるということは,分割の仕方および点
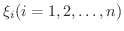 のとり方に関係なく一通りに定まるということです.これより,区分求積法とよばれ,次のようにして積分を求める方法があります.
のとり方に関係なく一通りに定まるということです.これより,区分求積法とよばれ,次のようにして積分を求める方法があります.
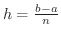 とすると,
とすると,
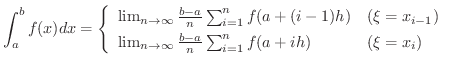
![$[a,b]$](img158.png) で積分可能になるのでしょうか.次の定理はそんな疑問に答えてくれます.
で積分可能になるのでしょうか.次の定理はそんな疑問に答えてくれます.
 が
が ![$[a,b]$](img158.png) で連続ならば,
で連続ならば, ![$[a,b]$](img158.png) で積分可能である.
で積分可能である.
今後,特に断らない限りこの章にでてくる 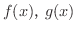 などの関数は,考えている区間で連続であるとします.
などの関数は,考えている区間で連続であるとします.
定積分の定義より,ただちに次の公式が得られます.
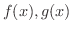 は区間
は区間 ![$[a,b]$](img158.png) で連続であるとすると,
で連続であるとすると,
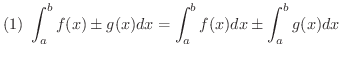
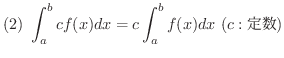
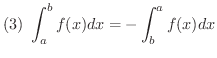
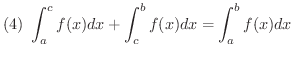
![$\displaystyle{(5) \ [a,b]\mbox{で} \ f(x) \geq g(x) \mbox{ならば,} \ \int_{a}^{b}f(x)dx \geq \int_{a}^{b}g(x)dx }$](img2338.png)
証明
(1)  の場合.
の場合. ![$[a,b]$](img158.png) の任意の分割を
の任意の分割を
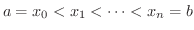
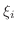 を
を
![$[x_{i-1},x_{i}]$](img2325.png) 内の任意の点としてRiemann和を考えると,
内の任意の点としてRiemann和を考えると,
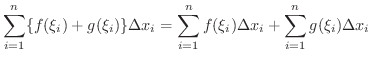
 とすると,定理3.7より,
とすると,定理3.7より,
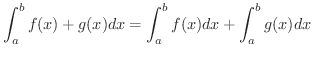
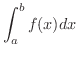 |
 |
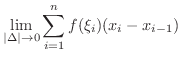 |
|
 |
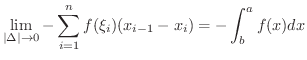 |

微分積分学の基本定理
関数  が
が ![$[a,b]$](img158.png) で連続であるとき,
で連続であるとき, ![$[a,b]$](img158.png) 内の任意の点
内の任意の点  に対して定積分
に対して定積分
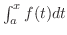 を考えると,これは
を考えると,これは ![$[a,b]$](img158.png) を定義域にもつ関数になります.この関数について,次の定理が成り立ちます.
を定義域にもつ関数になります.この関数について,次の定理が成り立ちます.
 が
が ![$[a,b]$](img158.png) で連続であれば,
で連続であれば,
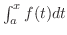 は
は  について微分可能であって,
について微分可能であって,
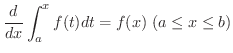
証明
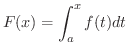 とおくと,
とおくと,
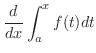 は
は 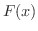 の導関数を求めることになるので,
の導関数を求めることになるので,
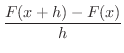 を考えます.まず,
を考えます.まず, 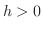 のとき,
のとき,
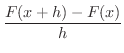 |
 |
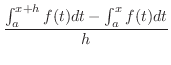 |
|
 |
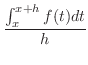 |
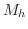 を
を ![$[x,x+h]$](img2356.png) における
における  の最大値,
の最大値, 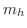 を
を ![$[x,x+h]$](img2356.png) における
における  の最小値とすると(なぜ最大値,最小値が存在するとわかる?),
の最小値とすると(なぜ最大値,最小値が存在するとわかる?), ![$[x,x+h]$](img2356.png) で
で
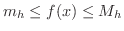
![$\displaystyle m_{h}[(x+h)-x] \leq \int_{x}^{x+h}f(t)dt \leq M_{h}[(x+h) - x] $](img2359.png)
 でわると,
仮定より,
でわると,
仮定より,  は
は ![$[x,x+h]$](img2356.png) で連続なので,
で連続なので,
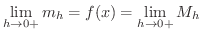
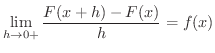
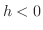 のとき
のとき
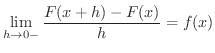
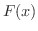 は微分可能であり,
は微分可能であり,
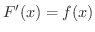 となる.
となる.

この定理より,
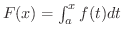 は
は  の原始関数となります.よって,連続な関数は必ず原始関数をもっていることがわかり,その原始関数は定積分で与えられます.
の原始関数となります.よって,連続な関数は必ず原始関数をもっていることがわかり,その原始関数は定積分で与えられます.
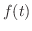 が連続のとき
が連続のとき
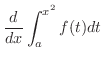
解
まず, 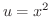 とおくと
とおくと
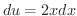 .よって
.よって
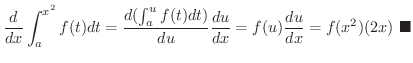
![$[a,b]$](img158.png) で連続な関数
で連続な関数  の
の 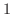 つの原始関数を
つの原始関数を 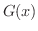 とすると
とすると
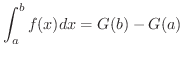
証明
定理3.7より,
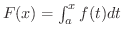 も
も  の原始関数です.よって,定理3.1より
の原始関数です.よって,定理3.1より
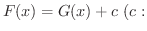 定数
定数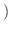 .
ここで
.
ここで 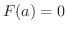 だから,
だから,
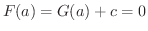 .よって,
.よって, 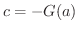 .
このとき
.
このとき
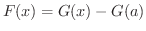 となるから,
となるから, 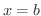 とすると,
とすると,
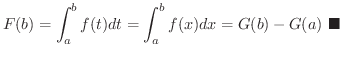
ここで,
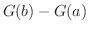 は
は
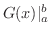 または
または
![$[G(x)]_{a}^{b}$](img2379.png) と略記されます.
と略記されます.
この定理より,定積分の計算は被積分関数の不定積分を求め,積分範囲の端点を代入しその差を求めればよいことがわかります.
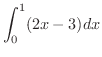
解
![$\displaystyle \int_{0}^{1}(2x -3)dx = \left[x^2 - 3x \right]_{0}^{1} = 1 - 3 = -2
\ensuremath{\ \blacksquare}
$](img2381.png)
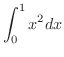 を求めよう.
を求めよう.
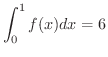 ,
,
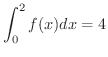 ,
,
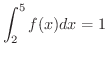 のとき,次の問いに答えよう.
のとき,次の問いに答えよう.
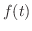 が連続であるとき,
が連続であるとき, 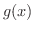 を求めよう.
を求めよう.
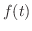 が連続であるとき,
が連続であるとき, 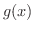 を求めよう.
を求めよう.