Next: 置換積分法(integration by substitution) Up: 積分法(INTEGRATION) Previous: 積分法(INTEGRATION) 目次 索引
ある区間で定義されている関数  に対して,この区間のすべての
に対して,この区間のすべての  について
について
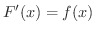
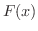 を
を  の 原始関数(primitive function) といいます.例えば,
の 原始関数(primitive function) といいます.例えば,
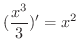 なので,
なので,
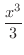 は
は
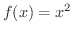 の原始関数です.同様に,
の原始関数です.同様に,
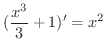 となるので
となるので
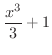 も
も
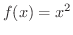 の原始関数です.ここで定数
の原始関数です.ここで定数  の導関数は0であることに注意すると
の導関数は0であることに注意すると
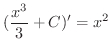 となり,
となり,
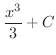 も
も
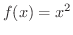 の原始関数です.この他にも
の原始関数です.この他にも
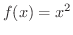 の原始関数はあるのでしょうか.そんな疑問に次の定理は答えてくれます.
の原始関数はあるのでしょうか.そんな疑問に次の定理は答えてくれます.
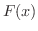 を
を  の原始関数の
の原始関数の 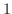 つとすると,
つとすると,  のすべての原始関数は
のすべての原始関数は 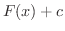 の形で与えられる.ただし
の形で与えられる.ただし 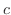 は任意の定数である.
は任意の定数である.
証明
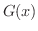 を
を  の任意の原始関数とすると,
の任意の原始関数とすると,
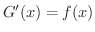 なので,
なので,
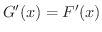 となります.したがって,系2.4より
となります.したがって,系2.4より
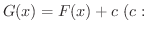 定数
定数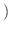
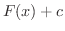 が
が  の原始関数であることは
の原始関数であることは
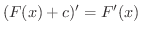 より明らかです.
より明らかです.

 の原始関数全体を
の原始関数全体を  の 不定積分(indefinite integral) といい,
の 不定積分(indefinite integral) といい,
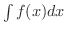 で表わします.つまり,
で表わします.つまり, 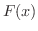 が
が  の原始関数の1つならば定理3.1より,
の原始関数の1つならば定理3.1より,
となります.また,
 の不定積分を求めることを,
の不定積分を求めることを,  を 積分する(integrate) といい,式3.1 に出てくる定数
を 積分する(integrate) といい,式3.1 に出てくる定数 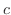 を 積分定数(constant of integration) といいます..なお不定積分を求めることができるできるということは,原始関数を初等関数だけを用いて表わすことができるということです.
を 積分定数(constant of integration) といいます..なお不定積分を求めることができるできるということは,原始関数を初等関数だけを用いて表わすことができるということです.
原始関数の定義をみると,変数が  であることは特別重要なことではないことに気づきます.例えば,関数
であることは特別重要なことではないことに気づきます.例えば,関数 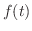 を考えてみてください.ここで
を考えてみてください.ここで  についての導関数が
についての導関数が
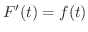 となる関数
となる関数 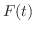 があれば,これは
があれば,これは 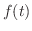 の原始関数となり,
の原始関数となり,
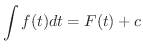
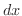 や
や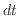 はどの変数について積分したかを表わしていて,ダミー変数(dummy variable) とよばれます.
はどの変数について積分したかを表わしていて,ダミー変数(dummy variable) とよばれます.
ここで,不定積分とは何かが分ったと思いますので,次の例題を見てみましょう.
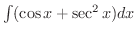 を求めてみましょう.
を求めてみましょう.
解
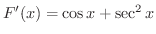 となる
となる 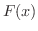 を求めます.
を求めます.
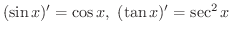
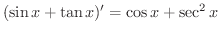
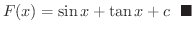
 を求めてみましょう.
を求めてみましょう.
解
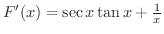 となる
となる 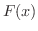 を求めます.
を求めます.
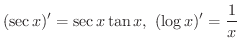
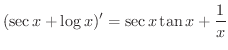
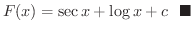
次に不定積分を求めるのに有用な基本的な公式をあげておきます.これらは右辺を微分することにより確かめることができます.
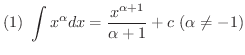
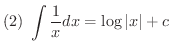
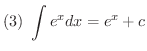
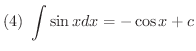
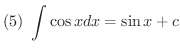
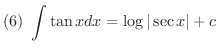
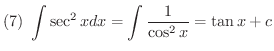
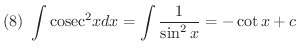
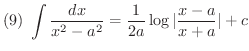
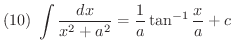
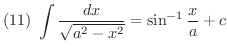
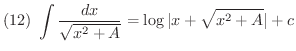
証明 (1)
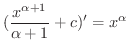 より
より
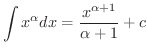
以下同様にして証明できます.

積分公式の(1)から(5)までは是非覚えましょう.(6)から(12)までは次に習う置換積分を用いることにより導くことができるので,できれば導き方を学びましょう.
積分公式を使って積分をするとき,次の定理は便利です.
 において,次の式が成り立つ.
において,次の式が成り立つ.
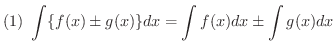
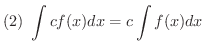
証明
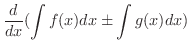 |
 |
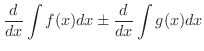 |
|
 |
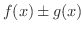 |
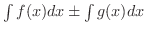 は
は
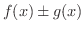 の不定積分です.
(2)の証明も同様にできます.
の不定積分です.
(2)の証明も同様にできます.

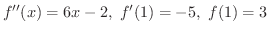 である
である を求めてみましょう.
を求めてみましょう.
解 まず,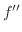 を積分することにより
を積分することにより
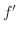 を求めます.
を求めます.
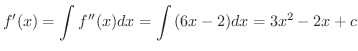
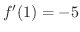 より,
より,
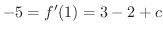 .したがって,
.したがって,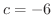 .これより,
.これより,
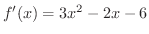 となります.
となります.
次に,
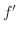 を積分して
を積分して を求めます.
を求めます.
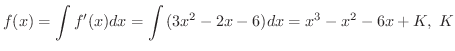 積分定数
積分定数
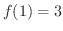 より,
より,
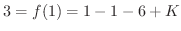 . したがって,
. したがって,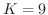 .これより,
.これより,
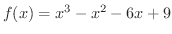

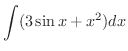 を求めてみましょう.
を求めてみましょう.
解
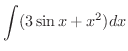 |
 |
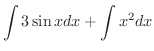 |
|
 |
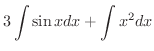 |
||
 |
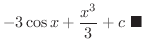 |