Next: 曲線の概形(curve sketching) Up: 微分法(DIFFERENTIATION) Previous: 高次導関数(higher-order derivatives) 目次 索引
連続関数の基本的性質として,中間値の定理と最大・最小値の定理がありました.では微分可能な関数の基本的性質としてどんなことがいえるのでしょうか.まず,フランスの数学者 Joseph Louis Lagrange (1736-1813) によって初めて証明された平均値の定理から始めましょう.
 が閉区間
が閉区間 ![$[a,b]$](img158.png) で連続で,開区間
で連続で,開区間 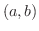 で微分可能ならば,
で微分可能ならば,
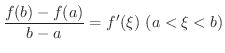
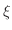 が少なくとも1つ存在する.
が少なくとも1つ存在する.
平均値の定理を証明する前に,平均値の定理はどんなことをいっているのか考えてみましょう.
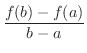 は2点
は2点
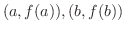 を結ぶ直線の傾きと考えることができます.すると,
を結ぶ直線の傾きと考えることができます.すると,
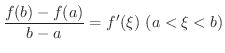
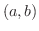 内に少なくとも1つあるということになります.ここで
内に少なくとも1つあるということになります.ここで  は走っている車の位置を表わしているとし,区間
は走っている車の位置を表わしているとし,区間 ![$[a,b]$](img158.png) は時間を表わしていると考えましょう.すると
は時間を表わしていると考えましょう.すると
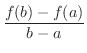 は時間
は時間 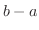 の間に走った距離を表わします.つまり,平均時速を表わしていることになります.では
の間に走った距離を表わします.つまり,平均時速を表わしていることになります.では
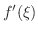 は何を表わしているのでしょうか.これは微小時間内の距離の変化.つまり瞬間の速さを表わしています.ちょうどねずみ取りのときに警察が使うレーザーの速度計に現われる車のスピードです.つまり,平均値の定理は平均時速が60kmならば,必ず一回は車のスピードメーターは時速60kmを指したことがあるはずだといっているのです.
は何を表わしているのでしょうか.これは微小時間内の距離の変化.つまり瞬間の速さを表わしています.ちょうどねずみ取りのときに警察が使うレーザーの速度計に現われる車のスピードです.つまり,平均値の定理は平均時速が60kmならば,必ず一回は車のスピードメーターは時速60kmを指したことがあるはずだといっているのです.
次に平均値の定理の特別な場合で フランスの数学者 Michel Rolle (1652-1719) によって1691年に発表された定理を考えます.
 が閉区間
が閉区間 ![$[a,b]$](img158.png) で連続,開区間
で連続,開区間 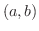 で微分可能で,さらに
で微分可能で,さらに
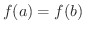 ならば,
ならば,
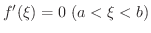
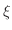 が少なくとも1つ存在する.
が少なくとも1つ存在する.
証明
最大・最小値の定理より,  は閉区間
は閉区間 ![$[a,b]$](img158.png) で最大値と最小値をとる.いま,
で最大値と最小値をとる.いま,
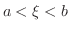 であるような点
であるような点 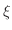 で最大値をとったとすると
で最大値をとったとすると
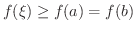 となる.これより,
となる.これより,
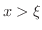 のとき
のとき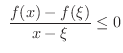
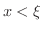 のとき
のとき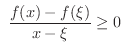
 は微分可能であるから,両不等式の左辺の極限値は
は微分可能であるから,両不等式の左辺の極限値は
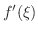 であり,次の2式が成り立つ.
であり,次の2式が成り立つ.
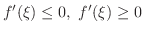
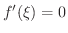
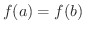 ならば,
ならば,
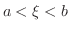 であるような点で最小値をとるから,いまと同様にして,
であるような点で最小値をとるから,いまと同様にして,
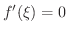 となる.
となる.

平均値の定理の証明
Rolleの定理の条件を満たすような関数を作る.2点
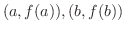 を結ぶ直線を
を結ぶ直線を 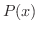 とすると,
とすると, 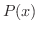 の方程式は
の方程式は
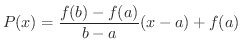
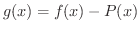 とおくと,
とおくと,
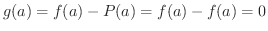 .また,
.また,
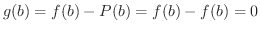 となり,Rolleの定理の条件を満たす.したがって,Rolleの定理より,
となり,Rolleの定理の条件を満たす.したがって,Rolleの定理より,
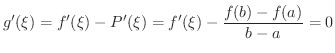
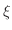 が少なくとも1つ存在する.
が少なくとも1つ存在する.

関数の性質
関数  が
が 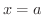 の近傍で定義されていて,
の近傍で定義されていて, 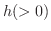 が十分小さいとき,つねに
が十分小さいとき,つねに
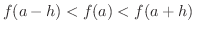 あるいは
あるいは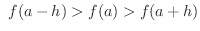
 はそれぞれ
はそれぞれ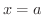 で増加の状態あるいは減少の状態にあるといいます.
で増加の状態あるいは減少の状態にあるといいます.
このような状態を簡単に見分ける方法はないのでしょうか.そんな疑問に次の定理は答えてくれます.
 が
が 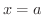 で微分可能であり,
で微分可能であり,
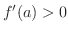 ならば,
ならば,  は
は 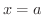 で増加の状態にあり,
で増加の状態にあり,
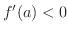 ならば,
ならば,  は
は 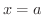 で減少の状態にある.
で減少の状態にある.
証明
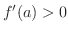 の場合を考え,
の場合を考え,
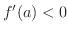 の場合は各自に任せます.
の場合は各自に任せます.
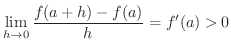
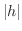 が十分小さければ,
が十分小さければ,
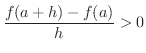
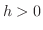 ならば
ならば
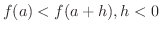 ならば
ならば
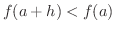 である.つまり,
である.つまり,  は
は 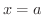 で増加の状態にある.
で増加の状態にある.

平均値の定理を利用して関数の性質を導いてみましょう.
 は閉区間
は閉区間 ![$[a,b]$](img158.png) で連続,開区間
で連続,開区間 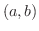 で微分可能とする.
で微分可能とする.
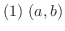 において,常に
において,常に
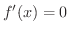 ならば
ならば  は
は ![$[a,b]$](img158.png) で定数関数.
で定数関数.
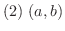 において,常に
において,常に
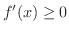 であって,しかも
であって,しかも 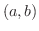 に含まれるどのような区間においても,
に含まれるどのような区間においても,
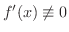 ならば,
ならば,  は
は ![$[a,b]$](img158.png) で狭義の単調増加関数である.
で狭義の単調増加関数である.
証明
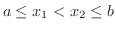 である任意の
である任意の
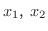 をとると,平均値の定理から
をとると,平均値の定理から
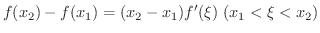
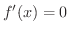 ならば,
ならば,
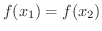 となり,
となり,  は定数関数である.
は定数関数である.
また常に
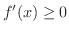 ならば,
ならば,
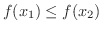 となる.もし,
となる.もし,
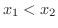 のとき
のとき
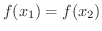 ならば,区間
ならば,区間
![$[x_{1},x_{2}]$](img1563.png) で定数関数となるから,そこで,
で定数関数となるから,そこで,
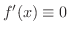 となって仮定に反する.したがって,
となって仮定に反する.したがって,
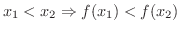
 は
は ![$[a,b]$](img158.png) で狭義の単調増加関数である.
で狭義の単調増加関数である.

 と
と 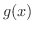 が閉区間
が閉区間 ![$[a,b]$](img158.png) で連続で,開区間
で連続で,開区間 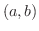 において,常に
において,常に
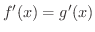 ならば,そこで
ならば,そこで
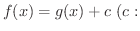 定数
定数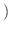
証明
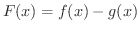 とおくと,
とおくと,
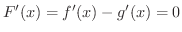 より
より 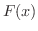 は定数関数.よって
は定数関数.よって
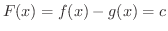 .
.

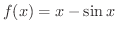 は
は
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img439.png) で狭義の単調増加関数であることを示してみましょう.
で狭義の単調増加関数であることを示してみましょう.
解
まず,
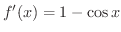 より,
より,
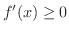 .また
.また
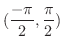 で
で
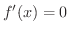 になるのは
になるのは  のときだけ.したがって,
のときだけ.したがって,  は
は
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img439.png) で狭義の単調増加関数となります.
で狭義の単調増加関数となります.

関数の大小を比較するにも,単調増加,単調減少が使えます.
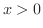 のとき,次の不等式が成り立つことを示してみましょう.
のとき,次の不等式が成り立つことを示してみましょう.
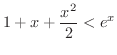
解
まず,
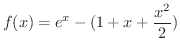 とおきます.
とおきます. より,不等式は
より,不等式は 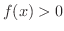 を示せば成り立つことがわかります.どうやったら示せるでしょうか.もし
を示せば成り立つことがわかります.どうやったら示せるでしょうか.もし
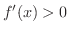 を示せれば,定理2.4より,
を示せれば,定理2.4より,  は狭義の単調増加関数となり,
は狭義の単調増加関数となり,  とあわせて,
とあわせて,
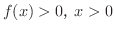 がいえます.そこで
がいえます.そこで
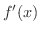 を求めると,
を求めると,
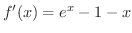
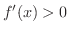 かわかりません.ところが
かわかりません.ところが
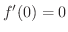 より,
より,
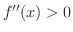 がいえれば,
がいえれば,
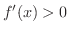 がいえます.そこで
がいえます.そこで
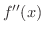 をもとめると
をもとめると
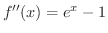
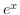 は
は 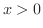 のとき,
のとき, 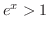 を満たすことをすでに学んだので
を満たすことをすでに学んだので
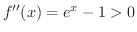 がいえます.よって,
がいえます.よって,
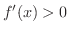 となり,これより,
となり,これより, 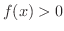 となります.
となります.

連続関数の性質として,ある区間での最大・最小値の定理がありましたが,ある点の近くでの関数の性質として,極大・極小は重要です.
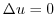 の近傍のすべての
の近傍のすべての  において
において
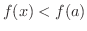 のとき,
のとき,  は
は 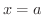 で極大(local maximum),
で極大(local maximum),
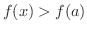 ならば
ならば  は
は 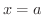 で極小(local minimum) であるといいます.また,
で極小(local minimum) であるといいます.また, 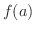 をそれぞれ極大値,極小値といい,両方をあわせて極値 (extrema) といいます.
をそれぞれ極大値,極小値といい,両方をあわせて極値 (extrema) といいます.
頭の中に微分可能な関数を思い浮かべてください.この曲線上の極値となるところで,微分係数または接線の傾きはどうなっているのか考えてみましょう.
 が
が 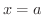 で微分可能で,かつこの点で極値をとれば,
で微分可能で,かつこの点で極値をとれば,
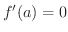 である.
である.
証明
もし
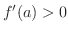 ならば,関数
ならば,関数  は
は 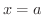 で増加の状態にあり,また
で増加の状態にあり,また
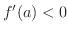 ならば,関数
ならば,関数  は
は 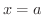 で減少の状態にある.したがって,どちらの場合にも
で減少の状態にある.したがって,どちらの場合にも 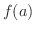 は極値にならない.ゆえに
は極値にならない.ゆえに
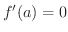 でなければならない.
でなければならない.

つまり微分可能な関数は極値をとる点では接線の傾きは0になることがわかりました.次に連続な関数はどんなときに極値をとるのか考えてみましょう.
 は
は 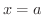 の近傍で連続で,
の近傍で連続で, 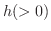 は十分小さいとする.
は十分小さいとする.
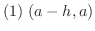 では
では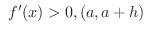 では
では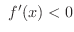 であるならば,
であるならば,  は
は 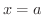 で極大になる.
で極大になる.
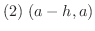 では
では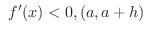 では
では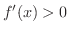 であるならば,
であるならば,  は
は 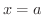 で極小になる.
で極小になる.
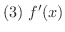 が
が 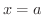 の前後で符号を変えなければ,
の前後で符号を変えなければ, 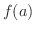 は極値でない.
は極値でない.
証明
定理2.4 により,  は区間
は区間 ![$[a-h,a]$](img1598.png) では狭義の単調増加関数,区間
では狭義の単調増加関数,区間 ![$[a,a+h]$](img1599.png) では狭義の単調減少関数になるから,
では狭義の単調減少関数になるから,  は
は 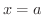 で極大になる.その他の場合の証明も同様にできます.
で極大になる.その他の場合の証明も同様にできます.

この定理から関数が微分可能でない点でも極値をとることがあることがわかったでしょうか.そんな例として
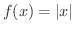 を考えてみましょう.
を考えてみましょう.
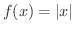 は
は  で微分可能ではありません.しかし
で微分可能ではありません.しかし  で極小値
で極小値  をとります.
をとります.
微分係数は接線の傾きを表わしていました.では2回微分係数はどんなことを表わしているのでしょうか.まずは2回微分係数とグラフの関係から考えましょう.
関数のグラフ上の点Pの近くで,グラフが点Pにおける接線(y軸に平行でない)の上側にあるとき,グラフは点Pで下に凸(concave up) であるといい,グラフが下側にあるとき上に凸(concave down) であるといいます.また,グラフが点Pの片側で接線の上側,もう片側では接線の下側にあるとき点Pを 変曲点(inflection point) といいます.
 が
が 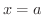 を含むある区間で
を含むある区間で 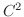 級で,
級で,
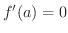
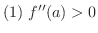 ならば,グラフは下に凸で
ならば,グラフは下に凸で 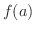 は極小値
は極小値
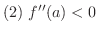 ならば,グラフは上に凸で
ならば,グラフは上に凸で 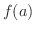 は極大値
は極大値
証明 (1)の証明. 関数
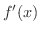 に定理2.4を適用すると,
に定理2.4を適用すると,
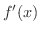 は
は 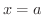 で増加の状態.いま,
で増加の状態.いま,
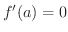 であるから,
であるから,
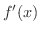 は
は 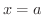 の近傍で左側では負,右側では正になる.よってグラフは下に凸となる.また定理2.4より,
の近傍で左側では負,右側では正になる.よってグラフは下に凸となる.また定理2.4より,  は
は 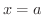 で極小.
(2)の証明も同様にできます.
で極小.
(2)の証明も同様にできます.

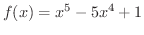 の極値およびグラフの凹凸を調べ,グラフの概形を描いてみましょう.また,区間
の極値およびグラフの凹凸を調べ,グラフの概形を描いてみましょう.また,区間 ![$[-1,1]$](img442.png) での最大値を求めてみましょう.
での最大値を求めてみましょう.
解
まず,  は
は
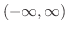 で微分可能より,極値をとれば,
で微分可能より,極値をとれば,
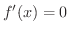 となります.そこで,
となります.そこで,
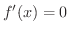 を満たす
を満たす  を求めます.
を求めます.
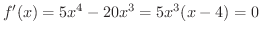
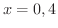 が極値の候補となります.次にグラフの凹凸を調べるため,
が極値の候補となります.次にグラフの凹凸を調べるため,
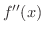 を求めます.
を求めます.
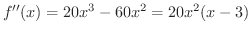
 軸上に,その下に
軸上に,その下に
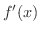 の符号,その下に
の符号,その下に
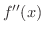 の符号,最後に
の符号,最後に  の増減を表わした,増減表とよばれる表を書いてみましょう.
の増減を表わした,増減表とよばれる表を書いてみましょう.
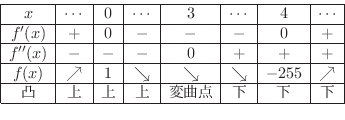
 で極大値
で極大値 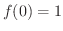 をとり,
をとり, 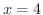 で極小値
で極小値
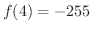 をとることがわかります.次に2回微分を用いると
をとることがわかります.次に2回微分を用いると 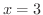 が変曲点で,その左側では上に凸,その右側では下に凸になっています.最後にグラフを描いてみましょう.
が変曲点で,その左側では上に凸,その右側では下に凸になっています.最後にグラフを描いてみましょう.
次に閉区間 ![$[-1,1]$](img442.png) を考えます.最大最小値の定理より,連続関数は閉区間の中で必ず最大値,最小値をとるので,端点
を考えます.最大最小値の定理より,連続関数は閉区間の中で必ず最大値,最小値をとるので,端点 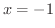 と
と 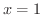 での値と区間
での値と区間 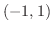 内での極大値,極小値を比べ,最も大きい値が最大値となります.よって
内での極大値,極小値を比べ,最も大きい値が最大値となります.よって
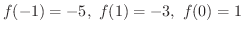
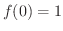 .
.

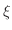 の値を求めよう.
の値を求めよう.
(a) 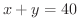 のとき,
のとき,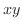 の最大値を求めよ.
の最大値を求めよ.
=2.6zw =1(b) 正四角形の2頂点が
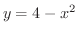 上にあり,残りの2頂点が
上にあり,残りの2頂点が 軸上にあるとき,正四角形の面積の最大値を求めよ.
軸上にあるとき,正四角形の面積の最大値を求めよ.
(c) 半径4の円に内接する正四角形の面積の最大値を求めよ.
(d) 楕円
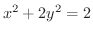 と直線
と直線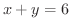 の最短距離を求めよ.
の最短距離を求めよ.
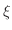 の値を,次の関数と区間について求めよう.
の値を,次の関数と区間について求めよう.
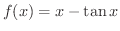 は
は
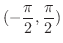 で狭義の単調減少関数となることを示そう.
で狭義の単調減少関数となることを示そう.