Next: 2.5 曲線の概形 Up: 確認問題解答 Previous: 2.3 高次導関数 目次 索引
1.
2.
(a)
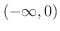 で上に凸,
で上に凸,
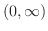 で下に凸,
で下に凸, 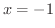 で極大値
で極大値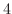 ,
,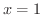 で極小値0, 変曲点
で極小値0, 変曲点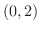
=2.6zw =1(c) 上に凸
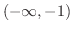 ,下に凸
,下に凸
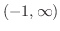 ,
,
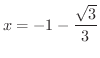 で極大値
で極大値
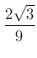 ,
,
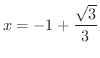 で極小値
で極小値
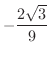 , 変曲点
, 変曲点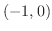
=2.6zw =1(d) 上に凸
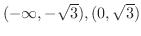 ,下に凸
,下に凸
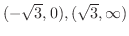 ,
, 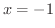 で極小値
で極小値
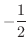 ,
,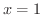 で極大値
で極大値
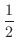 , 変曲点
, 変曲点
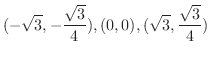
=2.6zw =1(e) 上に凸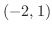 ,下に凸
,下に凸
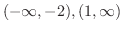 ,
, 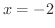 と
と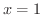 で極小値0,
で極小値0,
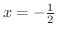 で極大値
で極大値
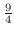
3.