Next: 不定形の極限値(limit of indeterminate forms) Up: 微分法(DIFFERENTIATION) Previous: 平均値の定理と関数の性質(mean-value theorem and properties 目次 索引
与えられた方程式が表わしている曲線の性質を調べ,その曲線の概形を描くことを考えましょう.そのためには次のことに注意しなければなりません.
問題によっては,まだ調べなければならないこともあり,またこのうちのいくつかを省いても実際に曲線の概形を描くことができることもあります.
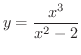 の概形を描いてみましょう.
の概形を描いてみましょう.
解
 の奇関数なので原点に対して対称となります.
の奇関数なので原点に対して対称となります.
 軸との交点は
軸との交点は 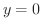 より
より  ,また
,また  軸との交点は
軸との交点は  より
より 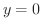 となり,原点でしか座標軸に交わりません.
となり,原点でしか座標軸に交わりません.
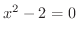 より
より
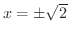 は漸近線です.次に
は漸近線です.次に
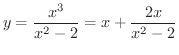
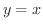 も漸近線です.
も漸近線です.
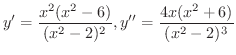
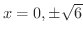 が極値の候補となります.ここで増減表を書くと
が極値の候補となります.ここで増減表を書くと
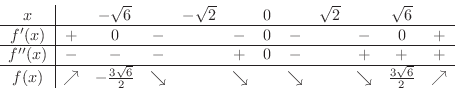
次に極座標で与えられた曲線の概形について考えてみましょう.まず,その前に極座標とは何なのかを学びましょう.
座標を用いる理由は点の位置を決めるためです.ただ,どういう基準で決めるかによって違ってきます.たとえば直交座標系では垂直に交わる2本の直線を基準に座標を決めます.極座標系(polar coordinate system) では 極(pole) とよばれる点と極からのびる極軸(polar axis) とよばれる軸によって座標を決めます.
直交座標平面上に1点P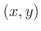 が与えられたとします.このとき点Pを極座標で表わすとどうなるでしょうか.まず,原点Oを極として極から点Pを通る光線を放ちます.このとき極軸とこの光線の作る角が
が与えられたとします.このとき点Pを極座標で表わすとどうなるでしょうか.まず,原点Oを極として極から点Pを通る光線を放ちます.このとき極軸とこの光線の作る角が 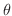 ならば,この光線を
ならば,この光線を 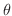 で表わします.次に極から点Pまでの距離を
で表わします.次に極から点Pまでの距離を 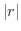 で表わします.すると,点Pの位置は
で表わします.すると,点Pの位置は 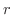 と
と 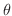 の組
の組
![$[r,\theta]$](img1650.png) によって完全に決めることができます.この
によって完全に決めることができます.この
![$[r,\theta]$](img1650.png) を点P
を点P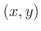 の 極座標(polar coordinate) とよびます.
の 極座標(polar coordinate) とよびます.
このとき点Pの直交座標 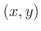 と極座標
と極座標
![$[r,\theta]$](img1650.png) の間には
の間には
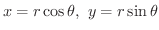
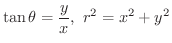
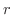 と
と 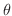 の値が与えられれば,点P
の値が与えられれば,点P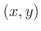 の位置は決まります.しかし,点P
の位置は決まります.しかし,点P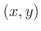 の位置が与えられても
の位置が与えられても 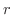 と
と 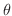 の値は一意的に定まりません.次の例題を考えてみましょう.
の値は一意的に定まりません.次の例題を考えてみましょう.
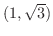 を極座標で表わしてみましょう.
を極座標で表わしてみましょう.
解
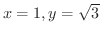 より
より
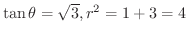 となります.これより点Pは光線
となります.これより点Pは光線
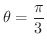 で極から点Pまでの距離は2となるので,点Pの極座標は
で極から点Pまでの距離は2となるので,点Pの極座標は
![$\displaystyle{[2,\frac{\pi}{3}]}$](img1657.png) と表わすことができます.ところが,光線
と表わすことができます.ところが,光線
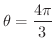 で
で 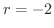 ととると点Pを表わすことができます.よって点Pの極座標は
ととると点Pを表わすことができます.よって点Pの極座標は
![$\displaystyle{[-2,\frac{4\pi}{3}]}$](img1660.png) .他にも
.他にも
![$\displaystyle{[2, \frac{7\pi}{3}]}$](img1661.png) などいろいろあります.図2.9参照
などいろいろあります.図2.9参照

曲線の方程式が直交座標で
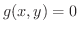
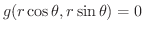
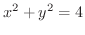 を極方程式で表わしてみましょう.
を極方程式で表わしてみましょう.
解
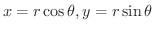 とおくと,
とおくと,
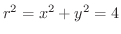 より
より 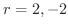

ここで極方程式の代表的なものをいくつか見てみましょう.
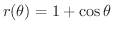 を描いてみましょう.
を描いてみましょう.
解
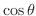 は偶関数より
は偶関数より
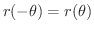 よって
よって  軸に対称.これよりグラフを描くには
軸に対称.これよりグラフを描くには
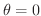 から
から
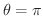 まで調べればよいことが分ります.
まで調べればよいことが分ります.
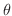 を 0 から
を 0 から 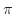 まで変化させたときの
まで変化させたときの 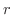 の変化を調べます.
の変化を調べます.
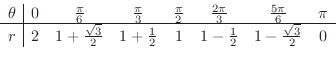
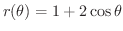 を描いてみましょう.
を描いてみましょう.
解
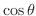 は偶関数より
は偶関数より
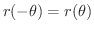 よって
よって  軸に対称.これよりグラフを描くには
軸に対称.これよりグラフを描くには
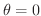 から
から
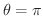 まで調べればよいことが分ります.
まで調べればよいことが分ります.
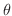 を 0 から
を 0 から 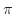 まで変化させたときの
まで変化させたときの 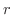 の変化を調べます.
の変化を調べます.
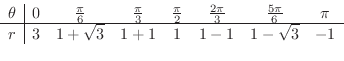
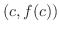 において,
において,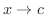 のとき,
のとき,
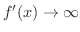 または
または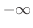 が成り立つことであり,垂直カスプとは,
が成り立つことであり,垂直カスプとは,
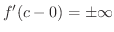 で
で
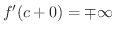 が成り立つことである.
が成り立つことである.
(a)
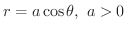 円(circle)
円(circle)
(b)
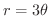 , アルキメデスの渦線(spiral)
, アルキメデスの渦線(spiral)
(c)
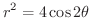 ベルヌーイのラムニスケイト(lemniscate)
ベルヌーイのラムニスケイト(lemniscate)