Next: 定積分(definite integral) Up: 積分法(INTEGRATION) Previous: 三角関数の積分法(integration of trigonometric functions) 目次 索引
無理関数の積分は残念ながらいつでも求められるとは限りません.ここでは適当な変換により,有理関数に帰着できるものを扱います.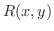 を
を 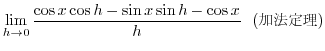 の有理関数とすると,
の有理関数とすると,
![$\displaystyle{(1) \ \int R(x,\sqrt[n]{\frac{ax+b}{cx+d}})dx}$](img2255.png) ,
,
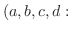 定数
定数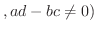 は
は
![$\displaystyle{t = \sqrt[n]{\frac{ax+b}{cx+d}}}$](img2258.png) より,有理関数になります.
より,有理関数になります.
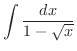 を求めてみましょう.
を求めてみましょう.
解
無理関数の積分は,無理関数を有理関数に変えれればよいので
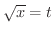 とおいてみましょう.すると
とおいてみましょう.すると 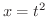 より
より
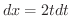 となります.よって
となります.よって
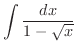 |
 |
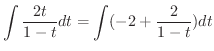 |
|
 |
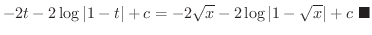 |
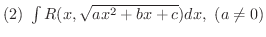 は
は
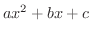 が
が
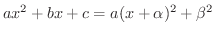 または
または
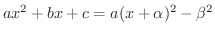 のいずれかで表わされます.そこで,
のいずれかで表わされます.そこで,
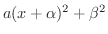 のときは斜辺が
のときは斜辺が
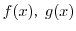 となるような直角三角形を考えます.
となるような直角三角形を考えます.
すると
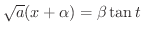 より
より
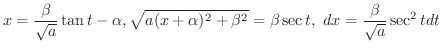
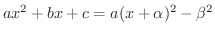 の場合は
の場合は
 が対辺となるような直角三角形を考えます.
が対辺となるような直角三角形を考えます.
すると
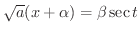 より
より
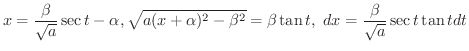
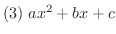 が実数解
が実数解
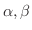 を持つときは,
を持つときは,
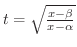 とおくと,
とおくと, と
と
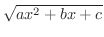 の有理関数の積分は
の有理関数の積分は の有理関数の積分に変換できます.
の有理関数の積分に変換できます.
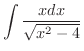 を求めてみましょう.
を求めてみましょう.
解
分母が2乗の差の平方根なので,これが対辺にくるような直角三角形を考えます.
すると
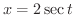 と表わせるので,
と表わせるので,
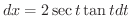 .また,
.また,
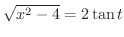 と表わせます.よって
と表わせます.よって
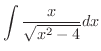 |
 |
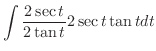 |
|
 |
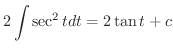 |
||
 |
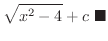 |
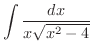 を求めてみましょう.
を求めてみましょう.
解
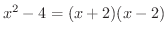 より,
より,
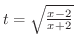 とおくと,
とおくと,
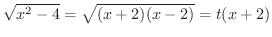 となります.両辺を2乗して
となります.両辺を2乗して について解くと,
について解くと,
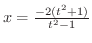 ,
,
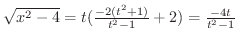 ,
,
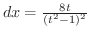 .
.
よって,
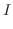 |
 |
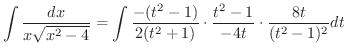 |
|
 |
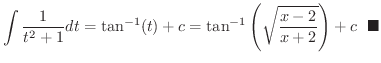 |