Next: 無理関数の積分法(integration of irrational functions) Up: 積分法(INTEGRATION) Previous: 有理関数の積分法(integration of rational functions) 目次 索引
前節ですべての有理関数は積分できることを学びました.そこで,三角関数の積分も三角関数を有理関数に直すことができればよいわけです.実は三角関数を有理関数に必ず直す方法があります.その最も一般的な方法として,
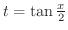 とおく置換があります.
とおく置換があります.
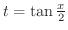 より,
より,
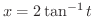 .次に,
.次に,
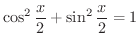
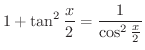
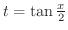 に注意すると
に注意すると
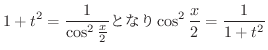
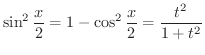
[1]
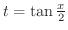 のとき,
のとき,
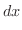 |
 |
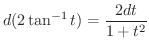 |
|
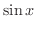 |
 |
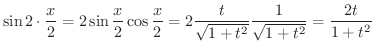 |
|
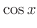 |
 |
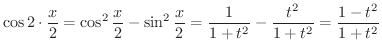 |
となり,すべての三角関数の積分は必ず有理関数の積分に直せます.しかし,この置換はあくまで最後に用いるもので,もっと簡単に有理関数に変えれる場合はそちらを用います.次のような場合があります.
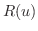 が
が 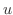 の有理関数のとき
の有理関数のとき
[2]
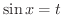 とおくと,
とおくと,
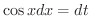 より,
より,
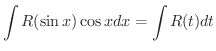
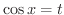 とおくと,
とおくと,
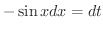 より,
より,
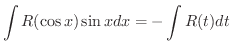
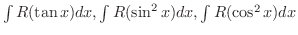 は
は
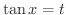 とおくと,
とおくと,
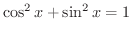 より
より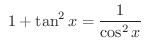
よって
[4]
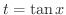 より,
より,
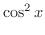 |
 |
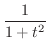 |
|
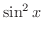 |
 |
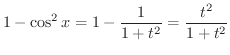 |
|
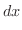 |
 |
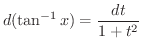 |
となり,  の有理関数に変換できます.
の有理関数に変換できます.
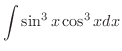 を求めてみましょう.
を求めてみましょう.
解
この積分は
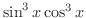 を
を
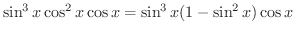
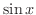 の有理関数と
の有理関数と 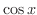 の積となります.そこで,
の積となります.そこで,
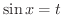 とおくことにより
とおくことにより
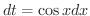 となり,
となり,  の有理関数に帰着することができます.よって
の有理関数に帰着することができます.よって
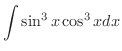 |
 |
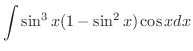 |
|
 |
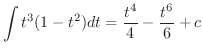 |
||
 |
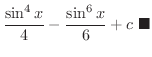 |
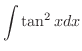 を求めてみましょう.
を求めてみましょう.
解
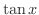 の有理関数は
の有理関数は
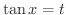 とおくと,
とおくと,
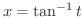 より
より
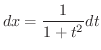
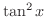 は
は  の有理関数.また,
の有理関数.また, 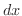 も
も  の有理関数と
の有理関数と 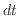 の積で表わせることがわかります.これより
の積で表わせることがわかります.これより
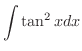 |
 |
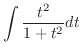 |
|
 |
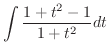 |
||
 |
![$\displaystyle \int [1 - \frac{1}{1+ t^2}] dt = t - \tan^{-1}{t} + c$](img2220.png) |
||
 |
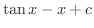 |
別解
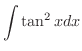 |
 |
 |
|
 |
 |
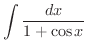 を求めてみましょう.
を求めてみましょう.
解
[2],[3],[4]のどちらの形もしていないので,最後の手段
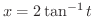 を用います.
を用います.
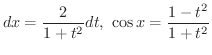
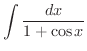 |
 |
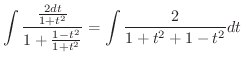 |
|
 |
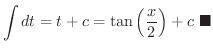 |