Next: 三角関数の積分法(integration of trigonometric functions) Up: 積分法(INTEGRATION) Previous: 部分積分法(integration by parts) 目次 索引
ここでは,有理関数の不定積分は必ず求めることができることを示しましょう.そこで,  ,
,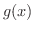 が整式のとき,その商
が整式のとき,その商
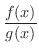 の不定積分について考えます.
の不定積分について考えます.
 の次数
の次数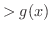 の次数 の場合は,
の次数 の場合は,  を
を 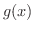 で割った商を
で割った商を 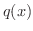 ,余りを
,余りを 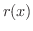 とすると,
とすると,
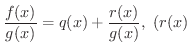 の次数
の次数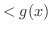 の次数
の次数
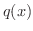 は整式なので,その積分は容易に求められます.そこで
は整式なので,その積分は容易に求められます.そこで  の次数
の次数 
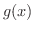 の次数の場合を考えます.
の次数の場合を考えます.
代数学の基本定理(fundamental theorem of algebra) によると,すべての整式は1次式と2次式の積で表わすことができます.よって 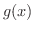 は次のように因数分解されます.
は次のように因数分解されます.
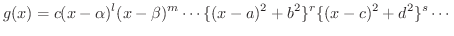
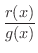 を部分分数分解します.部分分数分解(partial fraction) とは
を部分分数分解します.部分分数分解(partial fraction) とは
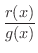 を分子の次数が分母の括弧内の次数より1次少ない分数で,その数が
を分子の次数が分母の括弧内の次数より1次少ない分数で,その数が 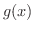 の因数の数となるように分解することをいいます.ちょっと分かりにくいので例を用いて説明します.まず,
の因数の数となるように分解することをいいます.ちょっと分かりにくいので例を用いて説明します.まず,
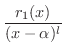 を部分分数分解してみましょう.
を部分分数分解してみましょう.
分母の因数の数は 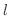 より,
より, 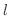 個の部分分数が必要となります.また,分母の括弧内の次数が1より分子は定数となることに注意すると,
個の部分分数が必要となります.また,分母の括弧内の次数が1より分子は定数となることに注意すると,
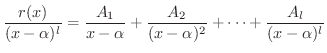
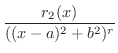 を部分分数分解してみましょう.
を部分分数分解してみましょう.
分母の因数の数は 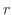 より,
より, 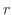 個の部分分数が必要となります.また,分母の括弧内の次数が2より分子は1次式となることに注意すると,
個の部分分数が必要となります.また,分母の括弧内の次数が2より分子は1次式となることに注意すると,
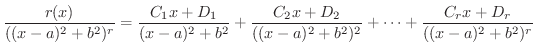
よって
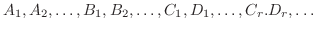 を求めます.これらの定数の求め方にはいろいろな方法が考案されています.2つほど紹介しましょう.
を求めます.これらの定数の求め方にはいろいろな方法が考案されています.2つほど紹介しましょう.
1つは  を両辺にかけて,分母を払います.すると両辺に多項式が生まれます.この多項式はすべての
を両辺にかけて,分母を払います.すると両辺に多項式が生まれます.この多項式はすべての  で等しいので,対応する係数どうしは等しくなければなりません.そこで左辺の
で等しいので,対応する係数どうしは等しくなければなりません.そこで左辺の  の係数と右辺の
の係数と右辺の 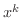 の係数を等しくおくことにより連立方程式が作れます.この連立方程式を解けば定数
の係数を等しくおくことにより連立方程式が作れます.この連立方程式を解けば定数
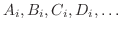 が求まり,部分分数分解が完成します.ただしこの方法は分母の次数が大きくなると連立方程式の数が増え,計算が煩雑になります.
が求まり,部分分数分解が完成します.ただしこの方法は分母の次数が大きくなると連立方程式の数が増え,計算が煩雑になります.
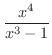
解 まず,分子の次数が分母の次数より大きいので,分子を分母で割ります.
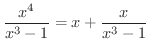
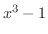 はまだ因数分解が可能なので因数分解し,部分分数分解すると
はまだ因数分解が可能なので因数分解し,部分分数分解すると
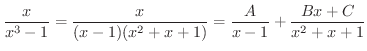
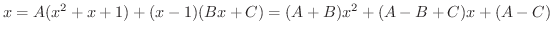
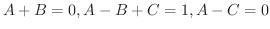
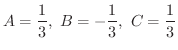 となります.
となります.

もう1つの方法は微分を用います.この方法は へービサイド展開(Heaviside expansion) とよばれています.
まず, 式3.2 の両辺に
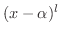 をかけると
をかけると
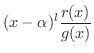 |
 |
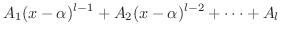 |
|
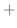 |
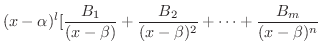 |
||
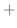 |
![$\displaystyle \frac{C_{1} x + D_{1}}{(x-a)^2 + b^2} + \frac{C_{2} x + D_{2}}{((x-a)^2 + b^2)^2} + \cdots + \frac{C_{r} x + D_{r}}{((x-a)^2 + b^2)^{r}} + \cdots ]$](img2077.png) |
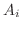 は
は
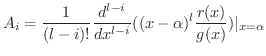
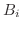 は
は
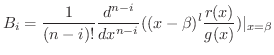
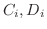 を求めるには
を求めるには
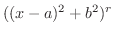 を 式3.2 の両辺にかけます.すると
を 式3.2 の両辺にかけます.すると
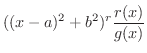 |
 |
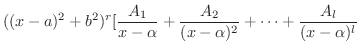 |
|
 |
![$\displaystyle \frac{B_{1}}{(x - \beta)} + \frac{B_{2}}{(x - \beta)^{2}} + \cdots + \frac{B_{m}}{(x - \beta)^{n}}]$](img2086.png) |
||
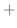 |
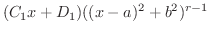 |
||
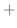 |
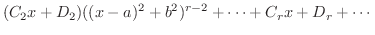 |
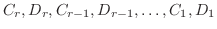 を求めることができます.
を求めることができます.
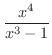
解 まず,分子の次数が分母の次数より大きいので,分子を分母で割ります.
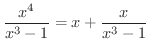
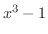 はまだ因数分解が可能なので因数分解し,部分分数分解すると
はまだ因数分解が可能なので因数分解し,部分分数分解すると
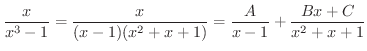
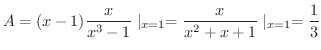
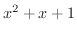 を両辺にかけ
を両辺にかけ
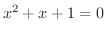 となるように
となるように  を選ぶと
を選ぶと
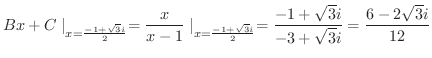
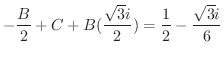
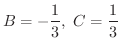 となります.
となります.

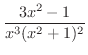
解
まず, 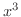 より
より 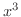 の3個の因数
の3個の因数 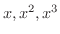 と,
と,
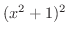 より
より
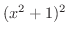 の2個の因数,
の2個の因数,
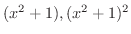 が分母をなす部分分数を用いて分解できます.つまり
が分母をなす部分分数を用いて分解できます.つまり
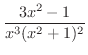 |
 |
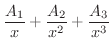 |
|
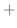 |
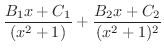 |
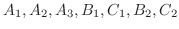 を求めます.
まず,
を求めます.
まず,
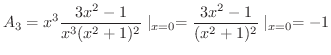
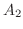 |
 |
![$\displaystyle \frac{d}{dx} [x^{3} \frac{3x^2 - 1}{x^3 (x^2 + 1)^{2}}]\mid_{x=0} = \frac{d}{dx}[\frac{3x^2 - 1}{(x^2 + 1)^{2}}]\mid_{x=0}$](img2106.png) |
|
 |
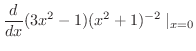 |
||
 |
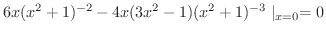 |
||
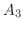 |
 |
![$\displaystyle \frac{1}{2!}\frac{d}{dx} [6x(x^2 + 1)^{-2} - 4x(3x^2 -1)(x^2 + 1)^{-3}]\mid_{x=0}$](img2110.png) |
|
 |
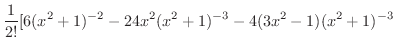 |
||
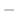 |
![$\displaystyle 24x^2 (x^2 +1)^{-3} - 4x(3x^2-1)(-6x(x^2 + 1)^{-4})]\mid_{x=0}$](img2112.png) |
||
 |
![$\displaystyle \frac{1}{2!}[6 + 4] = 5$](img2113.png) |
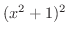 を両辺にかけると
を両辺にかけると
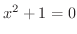 となるように
となるように  を選ぶと,
を選ぶと,
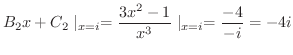
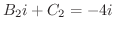 となり,これより
となり,これより
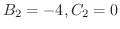 を得ます.
最後に
を得ます.
最後に
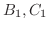 を求めます.式3.4を微分し,
を求めます.式3.4を微分し,
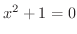 とおくと,
とおくと,
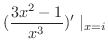 |
 |
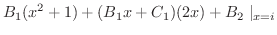 |
(3.5) |
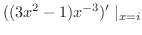 |
 |
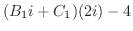 |
(3.6) |
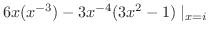 |
 |
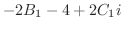 |
(3.7) |
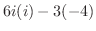 |
 |
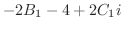 |
(3.8) |
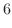 |
 |
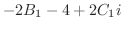 |
(3.9) |
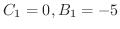 を得ます.
を得ます.

このように
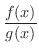 の部分分数分解はいくつかの次の形の分数の和として表わせます.
の部分分数分解はいくつかの次の形の分数の和として表わせます.
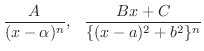
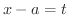 とおくと,次の形の関数に帰着します.
とおくと,次の形の関数に帰着します.
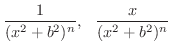
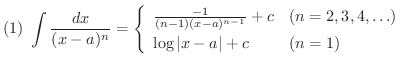
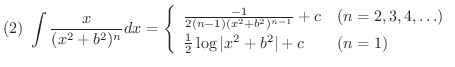
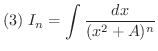 とおくと,次の漸化式が成り立つ.
とおくと,次の漸化式が成り立つ.
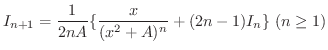
証明
(1) 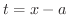 とおくt,
とおくt, 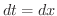 より
より
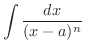 |
 |
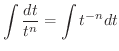 |
|
 |
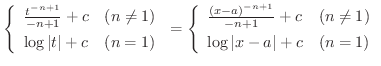 |
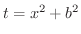 とおくt,
とおくt, 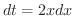 より
より
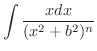 |
 |
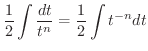 |
|
 |
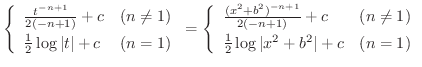 |
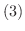 の証明.
の証明.
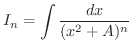 |
 |
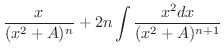 |
|
 |
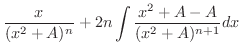 |
||
 |
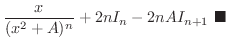 |
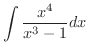 を求めてみましょう.
を求めてみましょう.
解 例題3.4より
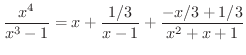
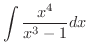 |
 |
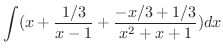 |
|
 |
![$\displaystyle \frac{1}{2}x^{2} + \frac{1}{3}\log{\vert x-1\vert} - \frac{1}{3}[\int \frac{x-1}{x^2 + x+ 1} dx]$](img2154.png) |
||
 |
![$\displaystyle \frac{1}{2}x^{2} + \frac{1}{3}\log{\vert x-1\vert} - \frac{1}{3}[\int \frac{x-1}{(x +\frac{1}{2})^{2} + \frac{3}{4}} dx]$](img2155.png) |
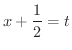 とおくと,
とおくと,
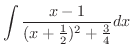 |
 |
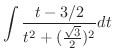 |
|
 |
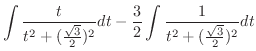 |
||
 |
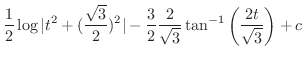 |
||
 |
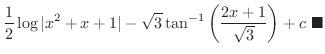 |