Next: 有理関数の積分法(integration of rational functions) Up: 積分法(INTEGRATION) Previous: 置換積分法(integration by substitution) 目次 索引
置換積分法を用いて.かなりの積分が求められるようになりました.しかし,
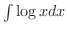 のような単純に思えるものも,置換積分法では手に負えないのです.実際,
のような単純に思えるものも,置換積分法では手に負えないのです.実際,
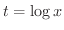 とおくと
とおくと
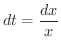 .これより,
.これより,
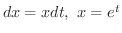 となり,
となり,
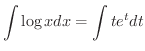
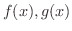 が連続であるとき,次の式が成り立つ.
が連続であるとき,次の式が成り立つ.
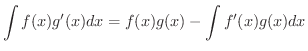
証明
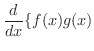 |
 |
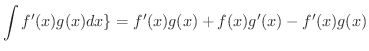 |
|
 |
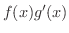 |
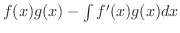 は
は
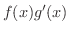 の不定積分となります.
の不定積分となります.

上の式で,
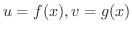 とおくと,次の式が成り立ちます.
とおくと,次の式が成り立ちます.
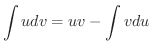
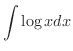 を求めてみましょう.
を求めてみましょう.
解
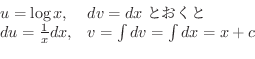
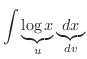 |
 |
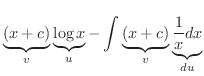 |
|
 |
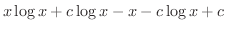 |
||
 |
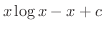 |
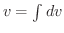 を求めるときは任意の定数
を求めるときは任意の定数 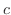 を無視できます.
を無視できます.

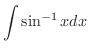 を求めてみましょう.
を求めてみましょう.
解
まず,
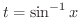 とおくと,
とおくと,
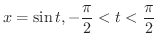 より,
より,
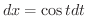 .よって
.よって
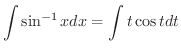
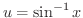 , , |
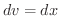 とおくと とおくと |
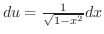 , , |
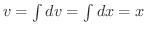 (定数cは無視) (定数cは無視) |
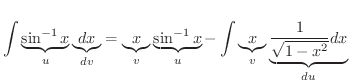
ここで,
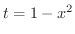 とおくと,
とおくと,
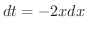 .よって
.よって
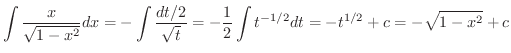
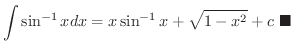
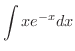 を求めてみましょう.
を求めてみましょう.
解
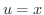 , , |
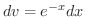 とおくと とおくと |
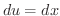 , , |
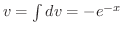 (定数cは無視) (定数cは無視) |
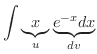 |
 |
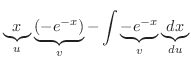 |
|
 |
 |