Next: オイラー e(Euler e)と超越関数 Up: 関数(FUNCTIONS) Previous: 連続関数(continuous functions) 目次 索引
自然数
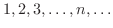 のおのおのの数に対してそれぞれ実数
のおのおのの数に対してそれぞれ実数
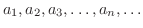
 などをこの数列の 項(term) といいます.特に第n項がわかれば数列全体がわかるので第n項を 一般項(general term) といいます.また,数列
などをこの数列の 項(term) といいます.特に第n項がわかれば数列全体がわかるので第n項を 一般項(general term) といいます.また,数列
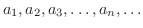 は簡単に
は簡単に  で表わされます.
で表わされます.
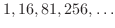 の第5項を求めてみよう,という問題が出題されたとき,ほとんどの学生は一般項
の第5項を求めてみよう,という問題が出題されたとき,ほとんどの学生は一般項
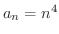 より,
より,
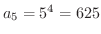 と答えました.ところがある学生は
と答えました.ところがある学生は
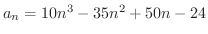 より
より
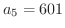 と答えました.どちらが正しいのか考えてみましょう.
と答えました.どちらが正しいのか考えてみましょう.
解
まず,
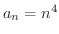 とおくと
とおくと
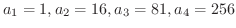 となるので
となるので
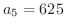 は正しい答です.では,
は正しい答です.では,
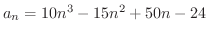 はどうでしょう.
はどうでしょう.
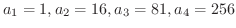 となるので
となるので
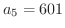 も正しい答です.
も正しい答です.

この答えを見て不思議だと思った人は,これまでに学んだ数列を思い出してみましょう.多分,等差数列と等比数列については学んだと思います.学んだことの無い人のために,それぞれの数列の定義を与えます.
 において,
において,
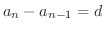 ただし,
ただし,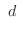 定数
定数
 は等差数列であるという.
は等差数列であるという.
 において,
において,
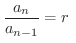 ただし,
ただし,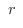 定数
定数
 は等比数列であるという.
は等比数列であるという.
つまり,等差数列や等比数列は隣り合う数列の差や比が一定の場合です.しかし,例題のように隣合う数列の差や比が一定でない数列の場合は,数列の差どうしの差を考える必要があります.これを階差といいます.次の数列を見てみましょう.
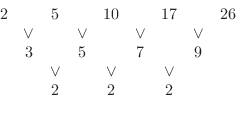
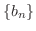 とすると,
とすると,
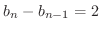 ,
, 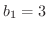 より,
より,
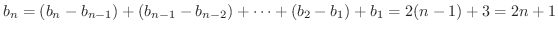
 とすると,
とすると,
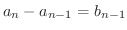 ,
, 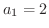 より,
より,
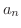 |
 |
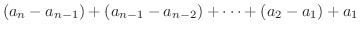 |
|
 |
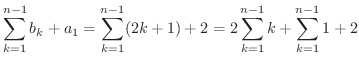 |
||
 |
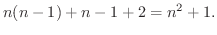 |
これより,数列 の一般項は
の一般項は
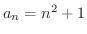 であると考えることができます.しかし,例題の数列の場合,階差を考えると,
であると考えることができます.しかし,例題の数列の場合,階差を考えると,
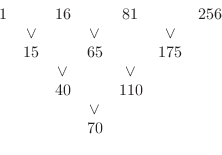
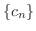 は,
は,
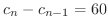 ,
,
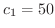 より,
より,
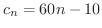 となります.これより,第2層目は
となります.これより,第2層目は
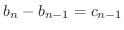 ,
,
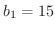 より,
より,
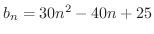 となります.したがって,第1層目は
となります.したがって,第1層目は
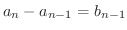 ,
, 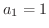 より,一般項は,
より,一般項は,
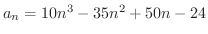 と考えることができます.
と考えることができます.
数列  において,すべての
において,すべての  について
について
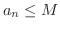 である定数
である定数 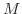 が存在するとき,数列
が存在するとき,数列  は 上に有界(bounded above) であるといい,すべての
は 上に有界(bounded above) であるといい,すべての  について
について
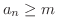 である定数
である定数 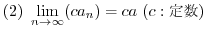 が存在するとき,数列
が存在するとき,数列  は 下に有界(bounded below) であるといいます.またすべての
は 下に有界(bounded below) であるといいます.またすべての  について
について
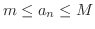 のとき,数列
のとき,数列  は 有界(bounded) であるといいます.
は 有界(bounded) であるといいます.
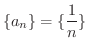 は 有界か調べてみましょう.
は 有界か調べてみましょう.
解
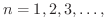 について
について
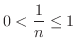

すべての  について
について
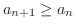 となるとき,数列
となるとき,数列  は 単調増加数列(monotonically increasing sequence) であるといいます.同様に,すべての
は 単調増加数列(monotonically increasing sequence) であるといいます.同様に,すべての  について
について
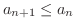 となるとき,数列
となるとき,数列  は 単調減少数列(monotonically decreasing sequence) であるといいます.
は 単調減少数列(monotonically decreasing sequence) であるといいます.
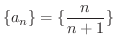 は単調増加数列か調べてみましょう.
は単調増加数列か調べてみましょう.
解
まず,どうやって 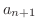 と
と 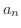 の大小の比較をしたらよいか考えてください.大きさの比較には,基本的に2つの方法があります.1つは差が正か負かを調べます.もう1つの方法は比が 1より大きいか小さいかを調べます.
の大小の比較をしたらよいか考えてください.大きさの比較には,基本的に2つの方法があります.1つは差が正か負かを調べます.もう1つの方法は比が 1より大きいか小さいかを調べます.
ここでは比を使って調べてみましょう.まず,
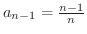 であることに注意して,
であることに注意して,
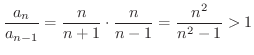
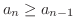 より,
より,  は単調増加であることがわかりました.
は単調増加であることがわかりました.

さて数列  において,項の番号が限りなく大きくなるとき,
において,項の番号が限りなく大きくなるとき, 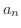 がある定数
がある定数  に限りなく近づくことを
に限りなく近づくことを
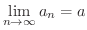
 は
は  に収束する(converge) といい,この
に収束する(converge) といい,この  を数列
を数列  の 極限値(limiting value)または 極限(limit) といいます.
の 極限値(limiting value)または 極限(limit) といいます.
ここで関数の極限値の考え方を用いると数列の極限値は次のように定義できます.
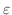 に対して,
に対して, 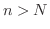 のとき
のとき
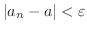 が成り立つような自然数
が成り立つような自然数 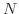 が存在するとき,数列
が存在するとき,数列  は
は  に収束するといい,
に収束するといい,
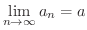
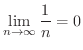 を証明してみましょう.
を証明してみましょう.
解
数列
 は任意の正の数
は任意の正の数
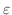 に対して
に対して
![$\displaystyle{N = [\frac{1}{\varepsilon} + 1]}$](img821.png) とおくと,
とおくと, 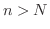 のとき
のとき
![$\displaystyle \vert a_{n} - 0\vert = \vert\frac{1}{n} - 0\vert = \vert\frac{1}{n}\vert < \frac{1}{N} = \frac{1}{[1/\varepsilon + 1]} < \varepsilon $](img822.png)
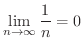
![$[x]$](img824.png) はガウス記号といい,
はガウス記号といい,  以下の整数のうち一番大きな整数を表します.
以下の整数のうち一番大きな整数を表します.

数列  が収束しないとき,数列
が収束しないとき,数列  は 発散する(diverge) といいます.関数の極限値と同じように次の定理は数列の極限値を求めるとき基本です.
は 発散する(diverge) といいます.関数の極限値と同じように次の定理は数列の極限値を求めるとき基本です.
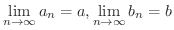 とすると,
とすると,
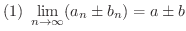
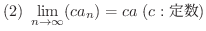
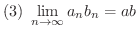
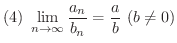
が成り立つ.
証明 定理1.3参照
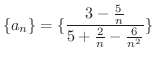 の極限値を求めてみましょう.
の極限値を求めてみましょう.
解
まず,
 のとき,
のとき,
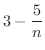
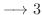 ,また
,また
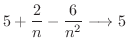 となります.したがって,
となります.したがって,
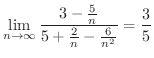

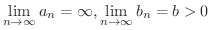 とすると,
とすると,
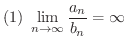
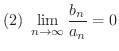
が成り立つ.
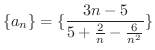 の極限値を求めてみましょう.
の極限値を求めてみましょう.
解
まず,
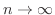 のとき,
のとき,
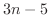
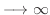 ,また
,また
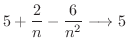 となります.したがって,
となります.したがって,
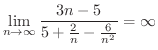

では,分子と分母が共に無限大に発散するときは,どうなるのでしょうか.このときの形を不定形(indeterminate)といい,このときは,分子と分母から の最高次数の項をくくり出すことによって,定理1.5,1.5を用いることができる形に変形します.
の最高次数の項をくくり出すことによって,定理1.5,1.5を用いることができる形に変形します.
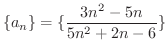 の極限値を求めてみましょう.
の極限値を求めてみましょう.
解
まず,
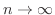 のとき,
のとき,
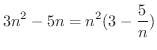
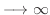 ,また
,また
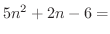
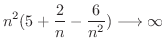 となります.そこで分子と分母から最高次数の項をくくりだすと
となります.そこで分子と分母から最高次数の項をくくりだすと
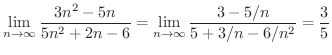

実際に極限値を求めるには上の定理1.5だけでは不十分です.例えば
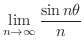 の極限値は定理1.5からは求められません.そんなとき,次の定理は便利です.
の極限値は定理1.5からは求められません.そんなとき,次の定理は便利です.
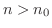 に対して
に対して
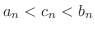 となる整数
となる整数 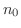 が存在し,
が存在し,
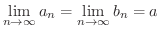
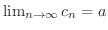 である.
である.
証明
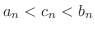 より
より
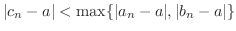
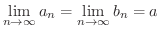
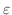 に対して自然数
に対して自然数  が存在し
が存在し
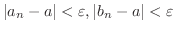
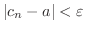 がいえる.よって
がいえる.よって
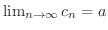 である.
である.

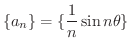 の極限を求めてみましょう.
の極限を求めてみましょう.
解
まず,
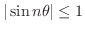 よりすべての
よりすべての 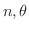 に対して
に対して
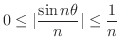
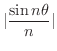 は 0 と
は 0 と
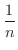 にはさまれました.ここで 0 と
にはさまれました.ここで 0 と
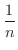 の極限値を求めると
の極限値を求めると
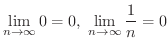
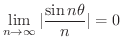
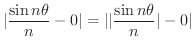
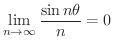

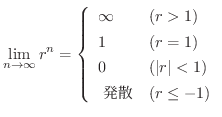
数列の収束,発散の基本となるものに 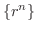 の極限がどうなるのか知っておく必要があります.なんとなく分かる人もいると思いますが,はっきりと理解したい人には,スイスの数学者 Jakob Bernoulli によって証明された Bernoulliの不等式(Bernoulli's inequality) と呼ばれる不等式は助けになるでしょう.
の極限がどうなるのか知っておく必要があります.なんとなく分かる人もいると思いますが,はっきりと理解したい人には,スイスの数学者 Jakob Bernoulli によって証明された Bernoulliの不等式(Bernoulli's inequality) と呼ばれる不等式は助けになるでしょう.
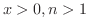 とすると,
とすると,
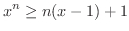
証明
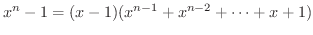
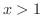 のとき
のとき 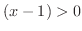 で
で
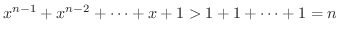
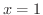 のとき
のとき 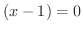 で
で
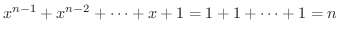
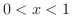 のとき
のとき 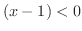 で
で
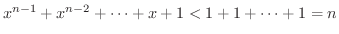
したがって,
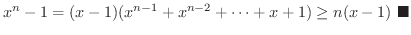
解
まず,
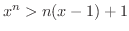 より
より 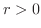 ならば
ならば
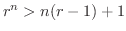 となります.
となります.
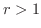 のとき
のとき
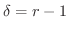 とおくと
とおくと
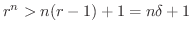 ,ここで
,ここで
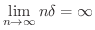
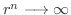 .
.
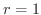 のとき
のとき
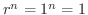 となるので
となるので
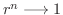 .
.
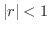 のときには
のときには
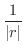 を考えます.
を考えます.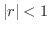 ならば,
ならば,
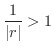 となるので
となるので
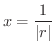 とおくとBernoulliの定理より
とおくとBernoulliの定理より
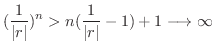
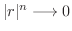 .これより
.これより
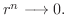
最後に 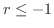 のとき
のとき
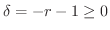 とおくとBernoulliの定理より
とおくとBernoulliの定理より
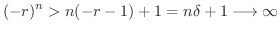
 が偶数のとき
が偶数のとき 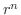 は大きな正の数となり
は大きな正の数となり  が奇数のときは
が奇数のときは 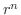 は絶対値が大きな負の数となります.このように正と負の間をいったりきたりしている数列を振動するといいます.
は絶対値が大きな負の数となります.このように正と負の間をいったりきたりしている数列を振動するといいます.

 の一般項を求めよう.
の一般項を求めよう.