Next: 連続関数(continuous functions) Up: 関数(FUNCTIONS) Previous: 初等関数(elementary functions) 目次 索引
関数の極限の話の前に,ギリシャの韋駄天Achillesとtortoiseの話をします.この話はZenon(B.C490-429)の逆説として人々を悩ませました.いろいろなかたちで伝わっていますが,ここではこれから極限を習うことを前提にした話にします.あるときAchilles(アキレス)がtortoise(カメ)を追いかけていました.アキレスがカメのいた位置に来たときにはカメはどんなに遅くともいささか前に進んでいます.次にアキレスがカメがいた位置に来たときには,またいささかでもとにかく前に進んでいます.この調子なので,アキレスはカメに追いつくことはできない,というのが,Zenonの逆説です.アキレスはカメに追いつけるのでしょうか.考えてみて下さい.
 において,
において,  を
を 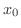 に限りなく近づけていくとき,
に限りなく近づけていくとき,  がある定数
がある定数 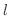 に限りなく近づくならば,
に限りなく近づくならば, 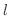 を
を  が
が 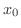 に近づくときの
に近づくときの  の 極限値(limit) といい,
の 極限値(limit) といい,
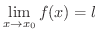
さて,ここで限りなく近づくというのはどういうことでしょうか. が
が 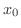 に限りなく近づくとは,絶対値
に限りなく近づくとは,絶対値
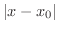 を限りなく小さくできるということと同じだと考えてもよいでしょう.同様に,
を限りなく小さくできるということと同じだと考えてもよいでしょう.同様に,  が定数
が定数 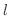 に限りなく近づくということも
に限りなく近づくということも
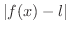 を限りなく小さくできることだと考えてもよいでしょう.そこで,限りなく小さくできるということで考えてみると,どんな小さな正の数を比較の相手と選んでも,それよりも小さくできるならば,限りなく小さくできるといえるのではないでしょうか.この考え方が数学でいうところの限りなく小さいということなのです(納得しましたか?).これを用いて関数の極限をもう一度定義します.この定義は
を限りなく小さくできることだと考えてもよいでしょう.そこで,限りなく小さくできるということで考えてみると,どんな小さな正の数を比較の相手と選んでも,それよりも小さくできるならば,限りなく小さくできるといえるのではないでしょうか.この考え方が数学でいうところの限りなく小さいということなのです(納得しましたか?).これを用いて関数の極限をもう一度定義します.この定義は
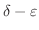 論法と呼ばれる証明法のもとになっていて,この章の定理の証明に用いますが,難しく感じる人は,直感的極限値で十分です.
論法と呼ばれる証明法のもとになっていて,この章の定理の証明に用いますが,難しく感じる人は,直感的極限値で十分です.
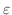 に対して,
に対して,
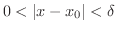 のとき,
のとき,
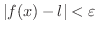 が成り立つように正の数
が成り立つように正の数 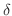 が選べるならば,
が選べるならば,
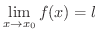
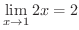 を証明してみましょう.
を証明してみましょう.
解
どんな
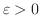 に対しても,
に対しても,
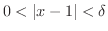 のとき
のとき
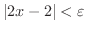 が成り立つような
が成り立つような 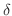 が存在することを示せばよいでしょう.そこで,
が存在することを示せばよいでしょう.そこで, 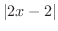 と
と 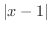 を比較すると
を比較すると
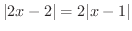
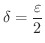 と選ぶと
と選ぶと
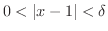 のとき
のとき
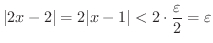

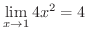 を証明してみましょう.
を証明してみましょう.
解
どんな
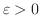 に対しても,
に対しても,
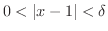 のとき
のとき
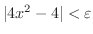 が成り立つような
が成り立つような 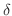 が存在することを示せばよいでしょう.そこで,
が存在することを示せばよいでしょう.そこで,
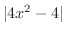 と
と 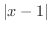 を比較すると
を比較すると
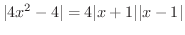
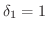 とおくと
とおくと
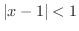 より
より
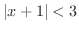 がいえるでしょう(確かめて).次に
がいえるでしょう(確かめて).次に
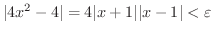
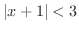 より
より
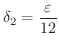 と選ぶ必要がでてきます.よって
と選ぶ必要がでてきます.よって
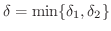 . つまり
. つまり 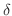 を
を
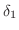 と
と
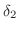 の小さいほうとなるように選ぶと,
の小さいほうとなるように選ぶと,
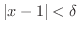 のとき
のとき
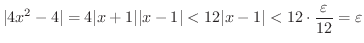

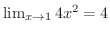 を定義にもとづいて証明するのは簡単ではありませんでした.そこで定義を使わずに極限値を求められるようになるように,次の定理を学びます.
を定義にもとづいて証明するのは簡単ではありませんでした.そこで定義を使わずに極限値を求められるようになるように,次の定理を学びます.
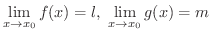 とすると,
とすると,
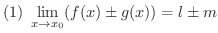
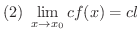
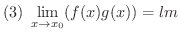
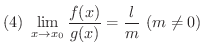
証明
(3)の証明. どんな
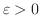 に対しても
に対しても
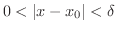 のとき,
のとき,
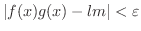 が成り立つような
が成り立つような
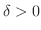 が存在することを示せばよいでしょう.
が存在することを示せばよいでしょう.
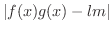 |
 |
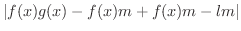 |
|
 |
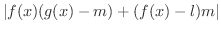 |
||
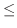 |
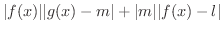 |
||
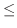 |
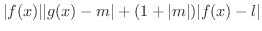 |
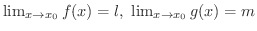 より,どんな
より,どんな
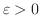 に対しても,
に対しても,
(i)
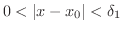 のとき,
のとき,
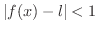 となる
となる
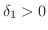 が存在する.
が存在する.
(ii)
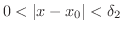 のとき,
のとき,
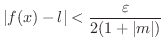 となる
となる
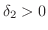 が存在する.
が存在する.
(iii)
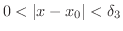 のとき,
のとき,
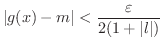 となる
となる
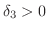 が存在する.
が存在する.
よって
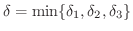 とすると,
とすると,
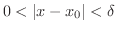 のとき,
のとき,
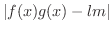 |
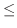 |
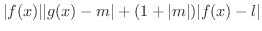 |
|
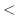 |
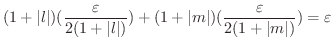 |

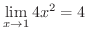 を見てみましょう.
を見てみましょう.
解
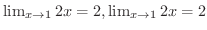 .よって定理1.3より
.よって定理1.3より
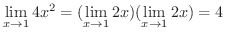

この定理の(4)は,有理関数の分母と分子の極限値が0でなければ,有理関数の極限値は分子と分母の極限値の商をとればよいといっています.では,分母の極限値が0だったらどうなるのでしょうか.まず,分母の極限値だけ0の場合について考えます.
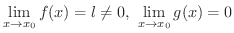 とすると,
とすると,
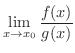
証明 もし,極限値が存在したら,
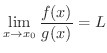
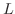 がある.したがって,
がある.したがって,
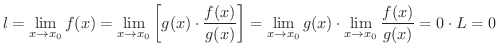
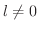 に矛盾する.したがって,
に矛盾する.したがって,
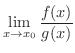

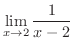 の極限値を求めてみましょう.
の極限値を求めてみましょう.
解 まず,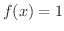 の極限値は
の極限値は
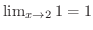 となります.次に,
となります.次に,
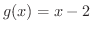 の極限値は
の極限値は
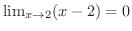 となります.したがって,定理1.3より,
となります.したがって,定理1.3より,
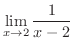 は存在しない.
は存在しない.
 では,分母と分子の極限値が共に0だったらどうなるのでしょうか.このときの形を不定形(indeterminate)といって,極限値の問題はいかに不定形の問題を解くかということに集約されます.
では,分母と分子の極限値が共に0だったらどうなるのでしょうか.このときの形を不定形(indeterminate)といって,極限値の問題はいかに不定形の問題を解くかということに集約されます.
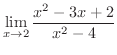 の極限値を求めてみましょう.
の極限値を求めてみましょう.
解
まず, 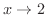 のとき,
のとき,
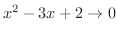 .また
.また
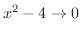 .つまり,分子,分母とも
.つまり,分子,分母とも 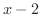 を共通因子に持っていることが分かります.そこで
を共通因子に持っていることが分かります.そこで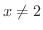 のとき,分子,分母から
のとき,分子,分母から 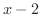 をくくりだすと
をくくりだすと
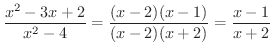
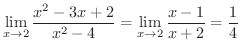

実際に極限値を求めるには上の定理だけでは不十分です.例えば,
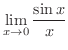 の極限値は上で用いた方法では求められません.そんなとき便利なものに,次のようなものがあります.
の極限値は上で用いた方法では求められません.そんなとき便利なものに,次のようなものがあります.
 の
の 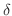 近傍
近傍
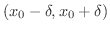 で
で
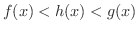 であって,
であって,
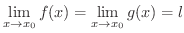
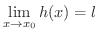 である.
である.
証明
どんな
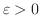 に対しても,
に対しても,
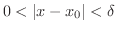 のとき,
のとき,
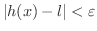 が成り立つような
が成り立つような
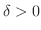 が存在することを示せばよいでしょう.
が存在することを示せばよいでしょう.
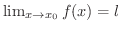 より,どんな
より,どんな
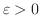 に対しても
に対しても
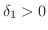 が存在し,
が存在し,
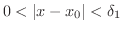 のとき,
のとき,
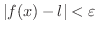 である.
である.
同様に,
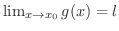 より,どんな
より,どんな
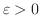 に対しても
に対しても
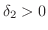 が存在し,
が存在し,
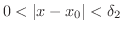 のとき,
のとき,
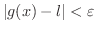 である.よって
である.よって
 とおくと,
とおくと,
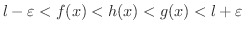
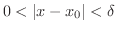 のとき,
のとき,
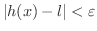 が成り立つ.
が成り立つ.

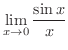 を求めてみましょう.
を求めてみましょう.
解
図1.12 において原点をOとし,単位円の周上に
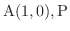 を取り, OP の延長線と OA に垂直な線の交点を B とします.またP から下ろした OA への垂線と OAの交点を Cとします.そのとき,面積を比較すると
を取り, OP の延長線と OA に垂直な線の交点を B とします.またP から下ろした OA への垂線と OAの交点を Cとします.そのとき,面積を比較すると
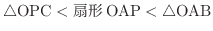 が成り立ちます.ここで,
が成り立ちます.ここで,
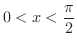 に対して,
に対して,
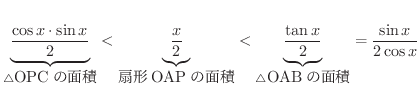
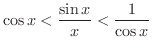
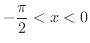 についても成り立ちます.さて,何を行ったかというと,
についても成り立ちます.さて,何を行ったかというと,
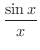 を2つの関数ではさみつけました.そして
を2つの関数ではさみつけました.そして
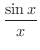 をはさむのに用いた
をはさむのに用いた 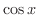 と
と
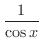 の
の
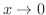 のときの極限値を調べると1になることが分かります.よって間にはさまれた
のときの極限値を調べると1になることが分かります.よって間にはさまれた
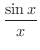 も
も
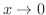 のときに1に近づくのではないか,というのがはさみうちの定理なのです.よって
のときに1に近づくのではないか,というのがはさみうちの定理なのです.よって
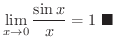
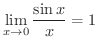 を用いて,
を用いて,
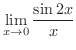 を求めてみましょう.
を求めてみましょう.
解
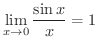 は,
は, が小さいとき,
が小さいとき,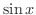 と
と はほぼ同じ大きさであることを示していることに注意する.
はほぼ同じ大きさであることを示していることに注意する.
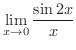 |
 |
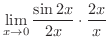 |
|
 |
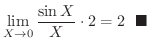 |