Next: 変数変換(change of variables) Up: 重積分法(MULTIPLE INTEGRATION) Previous: 2重積分(double integrals) 目次 索引
ここでは2重積分の計算について考えます.
2重積分をその定義に基づいて計算することは,2変数関数のRiemann和を求めて計算することに相当します.これは一般に困難なので,次の定理によって,2重積分を 累次積分(repeated integral) とよばれる単一積分の反復に変えて計算します.
(1)
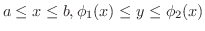 で囲まれた閉領域
で囲まれた閉領域
 で,
で,  が連続ならば
が連続ならば
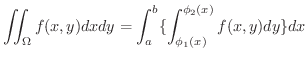
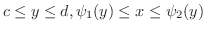 で囲まれた閉領域
で囲まれた閉領域
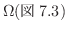 で,
で,  が連続ならば
が連続ならば
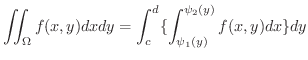
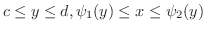 で囲まれた閉領域を 横線集合(H-simple) といいます.
で囲まれた閉領域を 横線集合(H-simple) といいます.
この定理は次のように考えることができます.
2重積分
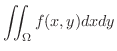
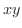 平面上の領域
平面上の領域  を底面とし,上面が
を底面とし,上面が
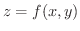 である柱状体の体積と考えられるので,その体積は
である柱状体の体積と考えられるので,その体積は
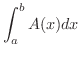
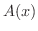 は
は  軸に垂直な平面で
軸に垂直な平面で
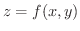 を切断した切断面の面積なので,縦方向に細長い長方形を積んでいくと考えると
を切断した切断面の面積なので,縦方向に細長い長方形を積んでいくと考えると
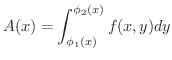
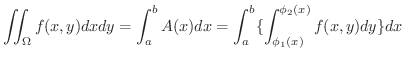
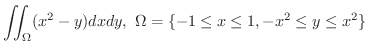
解
まず,  を図示(図7.5)すると
を図示(図7.5)すると
この領域はV-simpleなので,定理7.2(1)より
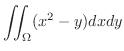 |
 |
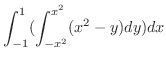 |
|
 |
![$\displaystyle \int_{-1}^{1}\left[(x^2 y - \frac{1}{2}y^2) \right ]_{-x^2}^{x^2} dx$](img3896.png) |
||
 |
![$\displaystyle \int_{-1}^{1}[(x^4 - \frac{1}{2}x^4) - (-x^4 - \frac{1}{2}x^4)]dx$](img3897.png) |
||
 |
![$\displaystyle \int_{-1}^{1}2x^4dx = \left[\frac{2}{5}x^5]\right ]_{-1}^{1} = \frac{4}{5}
\ensuremath{\ \blacksquare}$](img3898.png) |
 が図7.6 で与えられているとき,次の2重積分を求めてみましょう.
が図7.6 で与えられているとき,次の2重積分を求めてみましょう.
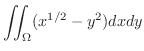
解 この領域はH-simpleでもありV-simpleでもあります.そこでまずV-simpleを用いて計算してみます.
V-simpleより  は次のように表わすことができます.
は次のように表わすことができます.
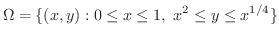
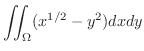 |
 |
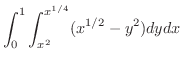 |
|
 |
![$\displaystyle \int_{0}^{1}\left[x^{1/2}y - \frac{1}{3}y^3]\right ]_{x^2}^{x^{1/4}}dx$](img3903.png) |
||
 |
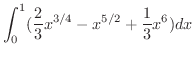 |
||
 |
![$\displaystyle \left[\frac{8}{21}x^{7/4} - \frac{2}{7}x^{7/2} + \frac{1}{21}x^7]\right ]_{0}^{1} = \frac{8}{21} - \frac{2}{7} + \frac{1}{21} = \frac{1}{7}$](img3905.png) |
次にこの積分をH-simpleを用いて行なってみます.この場合  は次のように表わすことができます.
は次のように表わすことができます.
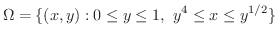
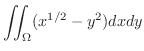 |
 |
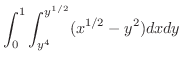 |
|
 |
![$\displaystyle \int_{0}^{1}\left[\frac{2}{3}x^{3/2} - y^2 x]\right ]_{y^4}^{y^{1/2}}dy$](img3908.png) |
||
 |
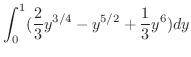 |
||
 |
![$\displaystyle \left[\frac{8}{21}y^{7/4} - \frac{2}{7}y^{7/2} + \frac{1}{21}y^7]\right ]_{0}^{1} = \frac{8}{21} - \frac{2}{7} + \frac{1}{21} = \frac{1}{7}$](img3910.png) |

このようにV-simpleで行なった積分をH-simple または H-simpleで行なった積分をV-simpleで行なうことを 積分順序の交換(change the order of integration)をするといいます.
(a) 曲面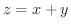 で上に有界で3点
で上に有界で3点
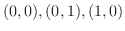 を頂点とする三角面で下に有界な立体
を頂点とする三角面で下に有界な立体
(b) 曲面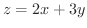 で上に有界で点
で上に有界で点
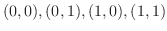 を頂点とする正方形で下に有界な立体
を頂点とする正方形で下に有界な立体
(c) 曲面
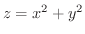 で上に有界で単位円盤
で上に有界で単位円盤
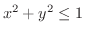 で下に有界な立体
で下に有界な立体
(d)
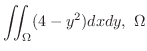 は
は 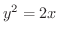 と
と
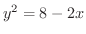 で囲まれた領域
で囲まれた領域