Next: 微分法(DIFFERENTIATION) Up: 関数(FUNCTIONS) Previous: オイラー e(Euler e)と超越関数 目次 索引
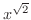 を定義するのに,上に有界な単調増加数列は収束するという定理を用いました.しかし,この定理の証明には実数の連続性が必要だということをいいました.また,中間値の定理,最大・最小値の定理の証明も実数の連続性がもとになっているといいました.そこでこの辺で,実数の連続性について考えてみましょう.
を定義するのに,上に有界な単調増加数列は収束するという定理を用いました.しかし,この定理の証明には実数の連続性が必要だということをいいました.また,中間値の定理,最大・最小値の定理の証明も実数の連続性がもとになっているといいました.そこでこの辺で,実数の連続性について考えてみましょう.
実数全体の集合
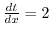 を私たちはよく数直線(number line) というものに置き換えて考えます.つまりすべての実数を大小の順に並べれば,どこにも穴のないぎっしりしたものになると考えます.集合
を私たちはよく数直線(number line) というものに置き換えて考えます.つまりすべての実数を大小の順に並べれば,どこにも穴のないぎっしりしたものになると考えます.集合
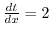 がこのような構造をもっていることを実数の連続性といいます.この実数の連続性を数学的にもっとはっきりした形のものとしてとらえることができないでしょうか.そのためにいろいろな方法が考えられていますが,私たちは上限,下限という概念に基づいて考えていくことにしましょう.
がこのような構造をもっていることを実数の連続性といいます.この実数の連続性を数学的にもっとはっきりした形のものとしてとらえることができないでしょうか.そのためにいろいろな方法が考えられていますが,私たちは上限,下限という概念に基づいて考えていくことにしましょう.
 に属するどんな実数
に属するどんな実数  に対しても
に対しても 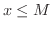 であるような数
であるような数 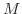 が存在するとき,
が存在するとき,  は 上に有界(bounded above) であるといい,このような数
は 上に有界(bounded above) であるといい,このような数 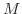 を
を  の 上界(upper bound) という.
の 上界(upper bound) という.
同様に,実数のある集合  に属するどんな実数
に属するどんな実数  に対しても
に対しても 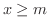 であるような数
であるような数  が存在するとき,
が存在するとき,  は 下に有界(bounded below) であるといい,このような数
は 下に有界(bounded below) であるといい,このような数 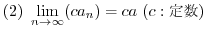 を
を  の 下界(lower bound) という.また上にも下にも有界な集合を単に有界(bouuded)な集合という.
の 下界(lower bound) という.また上にも下にも有界な集合を単に有界(bouuded)な集合という.
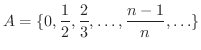
解
この集合には最小数はありますが最大数はありません.しかしこの集合のすべての数は 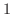 より小さいので
より小さいので 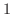 はこの集合の上界です.また,この集合のすべての数は 0 より大きいので 0 はこの集合の下界です.
はこの集合の上界です.また,この集合のすべての数は 0 より大きいので 0 はこの集合の下界です.

この集合をもう少しよく見てみましょう.この集合の中には 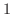 より小さいどんな数をとっても,それより大きい数がこの集合
より小さいどんな数をとっても,それより大きい数がこの集合  のなかにあります.つまり
のなかにあります.つまり 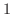 は上界の中で一番小さい数となります.このような数を上限といいます.
は上界の中で一番小さい数となります.このような数を上限といいます.
 の上界のうちで最小のものがある場合,その 最小な上界(least upper bound)を
の上界のうちで最小のものがある場合,その 最小な上界(least upper bound)を  の 上限(supremum) といい,
の 上限(supremum) といい, 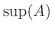 と表わす.また
と表わす.また  の下界のうちで最大のものがある場合,その 最大な下界(greatest lower bound)を
の下界のうちで最大のものがある場合,その 最大な下界(greatest lower bound)を  の 下限(infimum) といい,
の 下限(infimum) といい, 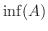 と表わす.
と表わす.
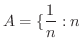 自然数
自然数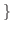
解
Aの上限は
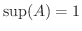 ,また下限は
,また下限は
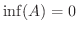

一般に,  に最大数
に最大数 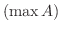 ,最小数
,最小数 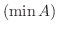 があるときは,それらはそれぞれ
があるときは,それらはそれぞれ の上限,下限になります.また
の上限,下限になります.また  の上限または下限が
の上限または下限が  に含まれているときには,それらはそれぞれ
に含まれているときには,それらはそれぞれ の最大数,最小数になります.
の最大数,最小数になります.
上の定義より,次の定理が得られます.
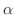 が
が  の上限であるというのは次の
の上限であるというのは次の  つの条件を共に満たしているということと同値である.
つの条件を共に満たしているということと同値である.
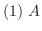 に属するすべての
に属するすべての  に対して,
に対して,
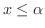 である.
である.
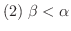 ならば
ならば
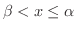 となるような
となるような  が
が  の中にある.
の中にある.
証明
(1)は 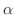 が
が  の上界であることを,(2)は
の上界であることを,(2)は 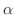 より小さい数は
より小さい数は  の上界になりえないことを表わしています.したがって,
の上界になりえないことを表わしています.したがって, 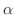 が
が  の上界のうちの最小数になる.
の上界のうちの最小数になる.

下限についても不等号の向きを逆にすれば同様です.
ここで実数全体の集合の基本的な性質をまとめておきます.
四則演算
任意の2つの数に対して,加減乗除の四則の演算が定義されていて,演算の結果がまた1つの実数になる.また交換,結合,分配などの法則が成り立つ.
大小関係
任意の実数 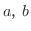 は
は
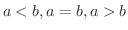 のうちどれか1つだけ成り立つ.また任意の実数
のうちどれか1つだけ成り立つ.また任意の実数 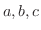 に対して,
に対して,
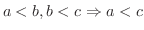
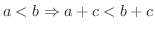
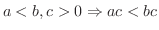
連続性
(1) 実数の集合  が上に有界ならば,
が上に有界ならば,  の上限が存在する.
の上限が存在する.
(2) 実数の集合  が下に有界ならば,
が下に有界ならば,  の下限が存在する.
の下限が存在する.
私たちは実数がこの3つの基本性質をもっているものとして話を進めていきます.このうちとくに連続性は実数で初めて成り立つ重要な性質です.例えば,
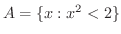 を考えると
を考えると  は上に有界なので,連続性より
は上に有界なので,連続性より  の上限が存在します.この場合
の上限が存在します.この場合  の上限は何でしょうか.定理1.7より
の上限は何でしょうか.定理1.7より 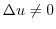 が
が  の上限となります.このように連続性を認めると有理数だけでは切れめができてしまう数直線の切れめをなくすことができます.
の上限となります.このように連続性を認めると有理数だけでは切れめができてしまう数直線の切れめをなくすことができます.
連続性をもとにして,集合
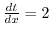 について直感的に認めてきた諸事実を1つずつ証明していくことができます.ここでは中間値の定理,数列の基礎定理を証明します.
について直感的に認めてきた諸事実を1つずつ証明していくことができます.ここでは中間値の定理,数列の基礎定理を証明します.
証明
数列  を上に有界な単調増加数列とする.実数
を上に有界な単調増加数列とする.実数 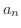 全体の集合を
全体の集合を  で表わすと,
で表わすと,  は上に有界となり,実数の連続性から
は上に有界となり,実数の連続性から  に上限が存在する.この上限を
に上限が存在する.この上限を 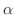 とすると定理より次の2つのことが成り立つ.
とすると定理より次の2つのことが成り立つ.
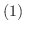 すべての
すべての  について
について
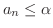
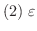 を任意の正の数とすると,
を任意の正の数とすると,
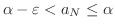 であるような
であるような 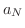 が
が  内に存在する.
内に存在する.
ここで  は単調増加だから,(2)における番号
は単調増加だから,(2)における番号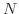 について,
について,
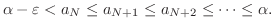
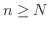 ならば
ならば
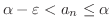 .したがって,
.したがって,
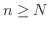 ならば,
ならば,
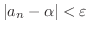 が成り立つ.ゆえに,
が成り立つ.ゆえに,
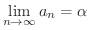

 が閉区間
が閉区間 ![$[a,b]$](img158.png) で連続ならば,
で連続ならば,
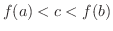 である任意の
である任意の 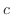 に対して,
に対して,
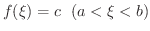
 が存在する.
が存在する.
証明
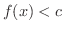 であるような
であるような  全体の集合を
全体の集合を  とする.つまり
とする.つまり
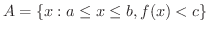 .
. は上に有界になるから上限が存在する.この上限を
は上に有界になるから上限が存在する.この上限を  とすると,
とすると,
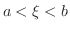 は明らかである.実はこの
は明らかである.実はこの  が
が
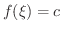 をみたす
をみたす  であることが次のようにして証明される.
まず仮に
であることが次のようにして証明される.
まず仮に
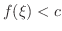 であるとすると,演習問題1.7 により,
であるとすると,演習問題1.7 により,  の適当な近傍をとることによって,そこでは
の適当な近傍をとることによって,そこでは 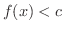 になる.つまり
になる.つまり
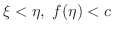
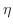 が存在する.ところがこれは
が存在する.ところがこれは  が
が  の上限であることに矛盾する.
の上限であることに矛盾する.
次に
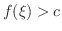 であるとすると,演習問題1.7 により,
であるとすると,演習問題1.7 により,  の適当な近傍をとることによって,そこでは
の適当な近傍をとることによって,そこでは 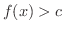 になる.つまり
になる.つまり
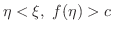
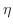 が存在する.ところがこれは
が存在する.ところがこれは  が
が  の上限であることに矛盾する.
の上限であることに矛盾する.
したがって,
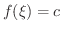 でなければならない.
でなければならない.

 が
が 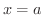 で連続で
で連続で
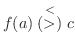 ならば,
ならば, 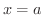 の十分近くで
の十分近くで
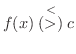 であることを示してみよう.
であることを示してみよう.