Next: 確認問題解答 Up: ベクトル解析(VECTOR ANALYSIS) Previous: 面積分(surface integrals) 目次 索引
残りの章ではベクトル積分定理とよばれる定理について学びます.これらの定理は簡単にいうと,閉領域の境界での関数の積分を,閉領域内部でのある微分演算子(勾配,発散,回転)を用いた積分で表わします.この関係の特殊な場合にすでに学んだ微分積分学の基本定理があります.つまり区間 ![$[a,b]$](img158.png) の端点での関数
の端点での関数  の値が,関数
の値が,関数  の導関数をその区間で積分したものと等しくなるというものです.つまり
の導関数をその区間で積分したものと等しくなるというものです.つまり
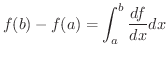
 と
と 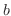 で微分演算子は導関数となります.
で微分演算子は導関数となります.
ここでは,2次元のベクトル場
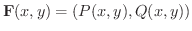
 がそれ自身で交わらない曲線上で積分します.このような閉曲線を 単一閉曲線(simple closed curve) といいます.
がそれ自身で交わらない曲線上で積分します.このような閉曲線を 単一閉曲線(simple closed curve) といいます.
1828年に イギリスの数学者 George Green (1793-1841) によって示された 平面上のGreenの定理 とよばれている定理について考えます.
 を境界にもつ
を境界にもつ  平面上の有界閉領域を
平面上の有界閉領域を  とする.またベクトル場
とする.またベクトル場
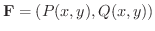 は
は 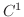 級とする.このとき
級とする.このとき
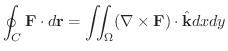
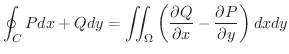
 の向きづけは進む方向に対して
の向きづけは進む方向に対して  が左側にくるものとする.
が左側にくるものとする.
証明
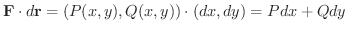
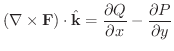
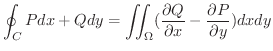
まず,領域  がV-simpleであり,またH-simpleでもあるとき標準領域とよぶことにします.つまり標準領域とは
がV-simpleであり,またH-simpleでもあるとき標準領域とよぶことにします.つまり標準領域とは
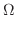 |
 |
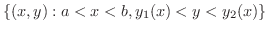 |
|
 |
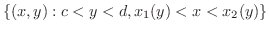 |
 が標準領域の場合について考えてみます.
が標準領域の場合について考えてみます.
 |
 |
![$\displaystyle \int_{a}^{b}\left[\int_{y_{1}(x)}^{y_{2}(x)}\frac{\partial P}{\partial y}dy\right] dx$](img4538.png) |
|
 |
![$\displaystyle \int_{a}^{b}[P(x,y_{2}(x)) - P(x,y_{1}(x))]dx$](img4539.png) |
||
 |
![$\displaystyle - \int_{a}^{b}[P(x,y_{1}(x)) - P(x,y_{2}(x))]dx$](img4540.png) |
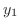 のグラフを左から右に進むようにパラメター
のグラフを左から右に進むようにパラメター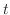 を用いて表わすと
を用いて表わすと
![$\displaystyle C_{1} : {\bf r}_{1}(t) = (t , y_{1}(t)), \ \ t \in [a,b] $](img4542.png)
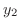 のグラフを左から右に進むようにパラメター
のグラフを左から右に進むようにパラメター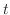 を用いて表わすと
を用いて表わすと
![$\displaystyle C_{2} : {\bf r}_{2}(t) = (t , y_{2}(t)), \ \ t \in [a,b] $](img4544.png)
 は正の方向に進むので,
は正の方向に進むので,
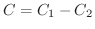 となる.よって
となる.よって
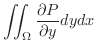 |
 |
![$\displaystyle - \int_{a}^{b}[P(x,y_{1}(x)) - P(x,y_{2}(x))]dx$](img4540.png) |
|
 |
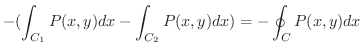 |
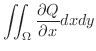 |
 |
![$\displaystyle \int_{c}^{d}\left[\int_{x_{1}(y)}^{x_{2}(y)}\frac{\partial Q}{\partial x}dx\right] dy$](img4548.png) |
|
 |
![$\displaystyle \int_{c}^{d}[Q(x_{2}(y),y) - Q(x_{1}(y),y)]dy$](img4549.png) |
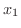 のグラフを下から上に進むようにパラメター
のグラフを下から上に進むようにパラメター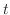 を用いて表わすと
を用いて表わすと
![$\displaystyle C_{3} : {\bf r}_{3}(t) = (x_{1}(t),t), \ \ t \in [c,d] $](img4550.png)
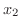 のグラフを下から上に進むようにパラメター
のグラフを下から上に進むようにパラメター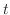 を用いて表わすと
を用いて表わすと
![$\displaystyle C_{4} : {\bf r}_{4}(t) = (x_{2}(t),t), \ \ t \in [c,d] $](img4551.png)
 は正の方向に進むので,
は正の方向に進むので,
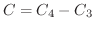 となる.よって
となる.よって
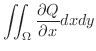 |
 |
![$\displaystyle \int_{c}^{d}[Q(x_{2}(y),y) - Q(x_{1}(y),y)]dy$](img4549.png) |
|
 |
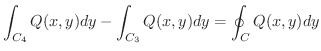 |
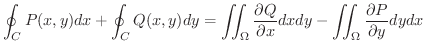
次に領域  が一般の場合を考えます.この場合
が一般の場合を考えます.この場合  を各部分が標準領域になるように分けると,
を各部分が標準領域になるように分けると,
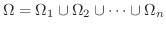
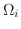 ではGreenの定理が成り立つので,その境界
ではGreenの定理が成り立つので,その境界
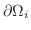 で
で
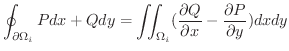
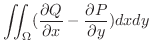
 の境界以外は打ち消しあって
の境界以外は打ち消しあって
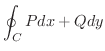
 についてGreenの定理が成り立つ.
についてGreenの定理が成り立つ.

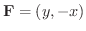 ,曲線
,曲線  を原点を中心とする半径1の円とする.このとき曲線
を原点を中心とする半径1の円とする.このとき曲線  に沿っての線積分
に沿っての線積分
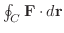 を Greenの定理を用いて求めてみましょう.
を Greenの定理を用いて求めてみましょう.
解
曲線  は
は
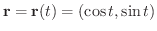 と表わせます.また
と表わせます.また  は半径1の円の内部より線積分は
は半径1の円の内部より線積分は
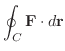 |
 |
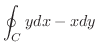 |
|
 |
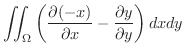 |
||
 |
 |
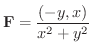 のとき,
のとき,
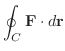 を求めてみましょう.ただし,曲線
を求めてみましょう.ただし,曲線  は例題8.6 と同じとします.
は例題8.6 と同じとします.
解
この問題のベクトル場  は
は 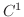 級ではありません.よってGreenの定理は使えません.そこで線積分
級ではありません.よってGreenの定理は使えません.そこで線積分
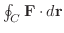 の計算を直接行わなければなりません.
の計算を直接行わなければなりません.
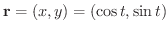
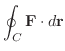 |
 |
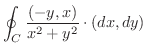 |
|
 |
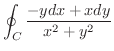 |
||
 |
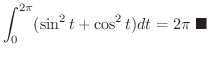 |
Stokesの定理
Greenの定理を アイルランドの数学者で物理学者の George Gabriel Stokes (1819-1903) が一般化したものをStokesの定理とよびます.まず, Stokesの定理を学ぶには,曲面の向きづけを行なう必要があります.
 上の各点
上の各点 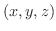 で法線ベクトル
で法線ベクトル
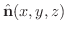 を適当に選び,
を適当に選び,
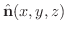 が
が  上で連続になるようにできるとき,曲面
上で連続になるようにできるとき,曲面  は 向きづけられる曲面(orientable)
という.また,このとき各点で選んだ
は 向きづけられる曲面(orientable)
という.また,このとき各点で選んだ
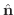 を,曲面の向きづけにより定まる法線単位ベクトルという.
を,曲面の向きづけにより定まる法線単位ベクトルという.
向きづけられた曲面  の境界の曲線
の境界の曲線
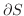 に沿っての線積分を,
に沿っての線積分を,  上での面積分に書き換える等式を与えるのがStokesの定理です.
上での面積分に書き換える等式を与えるのがStokesの定理です.
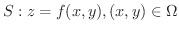 をいくつかの区分的に滑らかな閉曲線を境界とする向きづけられた曲面とする.また,ベクトル場
をいくつかの区分的に滑らかな閉曲線を境界とする向きづけられた曲面とする.また,ベクトル場  は
は  上で
上で 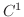 級とする.そのとき,
級とする.そのとき,
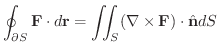
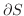 は
は  の境界を表わし,曲線
の境界を表わし,曲線
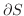 上の線積分の向きは領域
上の線積分の向きは領域  を左手にみるように
を左手にみるように
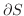 を一周するものとする.つまり,法線単位ベクトル
を一周するものとする.つまり,法線単位ベクトル
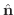 に対して右手の法則に従う.
に対して右手の法則に従う.
証明
まず,
![$\iint_{S} [\nabla \times F_{1}\hat{\bf i}] \cdot \hat{\bf n}dS$](img4578.png) を考えよう.
を考えよう.
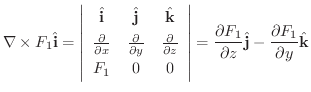
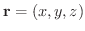 を位置ベクトルとすると,
を位置ベクトルとすると,
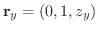 は
は  の接線ベクトルとなるので,法線ベクトル
の接線ベクトルとなるので,法線ベクトル
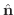 とは直交する.よって
とは直交する.よって
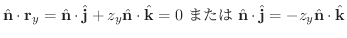
![$\displaystyle [\nabla \times F_{1}\hat{\bf i}] \cdot \hat{\bf n}dS = - \left (\...
... + \frac{\partial F_{1}}{\partial y} \right ) \hat{\bf n} \cdot \hat{\bf k} dS $](img4583.png)
 上では
上では
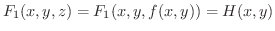 とおけるので合成関数の微分法より
とおけるので合成関数の微分法より
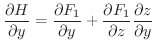
![$\displaystyle [\nabla \times F_{1}\hat{\bf i}] \cdot \hat{\bf n}dS = - \frac{\p...
...tial y}\hat{\bf n} \cdot \hat{\bf k} dS = - \frac{\partial H}{\partial y}dx dy $](img4586.png)
![$\displaystyle \iint_{S}[\nabla \times F_{1}\hat{\bf i}] \cdot \hat{\bf n}dS = \iint_{\Omega}- \frac{\partial H}{\partial y}dx dy $](img4587.png)
 は
は  を
を  平面に正射影したものである.右側の積分は平面上の積分で,Greenの定理より
平面に正射影したものである.右側の積分は平面上の積分で,Greenの定理より
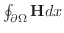 となる.
となる. の境界上の点
の境界上の点 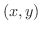 での
での 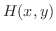 の値と,
の値と,  の境界上の点
の境界上の点 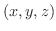 での
での
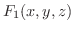 の値は等しく,また,
の値は等しく,また, 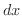 はどちらの曲線でも同じなので,
はどちらの曲線でも同じなので,
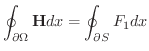
![$\displaystyle \iint_{S}[\nabla \times F_{1}\hat{\bf i}] \cdot \hat{\bf n}dS = \oint_{\partial S}{F_{1}}dx $](img4592.png)
![$\displaystyle \iint_{S}[\nabla \times F_{2}\hat{\bf j}] \cdot \hat{\bf n}dS = \...
...bla \times F_{3}\hat{\bf k}] \cdot \hat{\bf n}dS = \oint_{\partial S}{F_{3}}dz $](img4593.png)
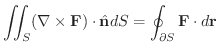

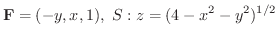 のとき,Stokesの定理が成り立つことを示してみましょう.
のとき,Stokesの定理が成り立つことを示してみましょう.
解
 の境界
の境界
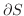 は
は
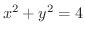 の円となります.よって位置ベクトル
の円となります.よって位置ベクトル
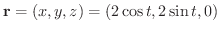 より線積分を求めると
より線積分を求めると
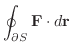 |
 |
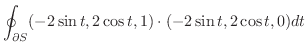 |
|
 |
![$\displaystyle \int_{0}^{2\pi}[4\sin^{2}{t} + 4\cos^{2}{t}]dt = 8\pi$](img4600.png) |
次に面積分を求めてみます.
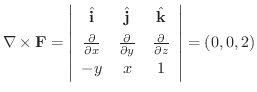
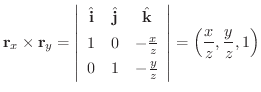
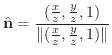
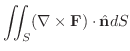 |
 |
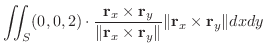 |
|
 |
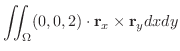 |
||
 |
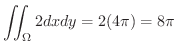 |

これまでに保存場では,ベクトル場はスカラー場の勾配と等しくなり,またベクトル場の回転は0になることをすでに学びました.では線積分との関係においては,どんなことが成り立つのか調べてみましょう.
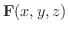 では次の 3つの条件は同値である.
では次の 3つの条件は同値である.
(1)
 となるスカラー関数
となるスカラー関数
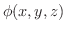 が存在する.(Fは保存場)
が存在する.(Fは保存場)
(2) いたるところ
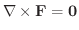 が成り立つ.(渦なし)
が成り立つ.(渦なし)
(3) 任意の閉曲線  について
について
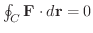 が成り立つ (積分経路無関係).
が成り立つ (積分経路無関係).
証明
(1)
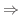 (2)
(2)
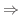 (3)
(3)
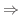 (1)を示す.
(1)を示す.
(1)
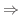 (2)
(2)
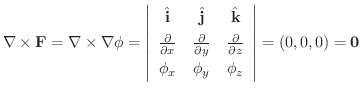
(2)
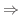 (3) 閉曲線
(3) 閉曲線  で囲まれた曲面
で囲まれた曲面  を考えて,Stokesの定理を使うと
を考えて,Stokesの定理を使うと
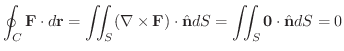
(3)
 (1) 定点P
(1) 定点P
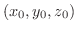 と動点Q
と動点Q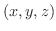 をむすぶ2つの曲線
をむすぶ2つの曲線
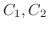 をとり,Pから
をとり,Pから 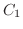 を経てQに至り,Qから
を経てQに至り,Qから 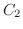 を逆向きに通ってPに戻る道を
を逆向きに通ってPに戻る道を  とすると,
とすると,
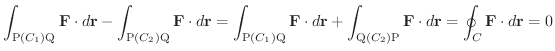
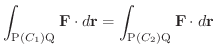
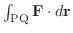 は途中の経路に関係なく,終点Qの座標
は途中の経路に関係なく,終点Qの座標 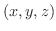 の関数で与えられる.よってこれを
の関数で与えられる.よってこれを
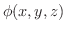 とすれば,
とすれば,
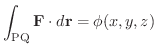
PからQに至る任意の曲線のベクトル方程式を
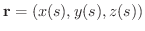 とすると,
とすると,
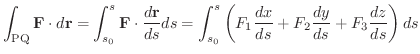
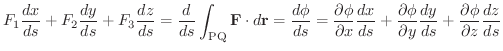
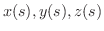 も任意の関数でよいから,
も任意の関数でよいから,
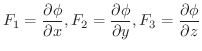
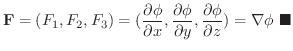
この定理より,線積分をおこなうときに,ベクトル場がスカラーポテンシャルを持てば,積分をしなくとも答は0であることが分かります.
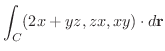 を求めてみましょう.ただし,
を求めてみましょう.ただし,  は点
は点 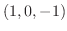 から点
から点 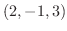 に至る曲線.
に至る曲線.
解
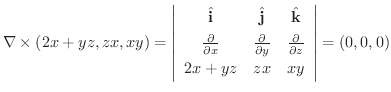
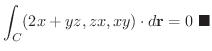
次にドイツの数学者 Karl Friedrich Gauss (1777-1855) の名前をとってつけられた発散定理について学びます.
Gaussの発散定理
 において,区分的に滑らかな閉曲面
において,区分的に滑らかな閉曲面  で囲まれた空間の領域を
で囲まれた空間の領域を 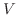 とし,
とし,  の内部から外部に向かう法線ベクトルを
の内部から外部に向かう法線ベクトルを
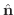 とすると,
とすると,
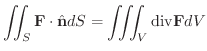
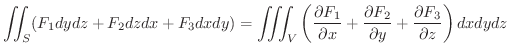
証明 まず, 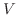 が2つの曲面
が2つの曲面
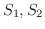 で下と上からはさまれているとします.また,
で下と上からはさまれているとします.また, 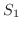 は
は
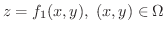 ,
, 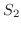 は
は
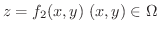 で与えられているとします.このとき,
で与えられているとします.このとき,
 |
 |
![$\displaystyle \iiint_{V}\frac{\partial F_{3}}{\partial z} dzdydx = \iint_{\Omega}[\int_{z=f_{1}(x,y)}^{f_{2}(x,y)}\frac{\partial F_{3}}{\partial z} dz] dydx$](img4644.png) |
|
 |
![$\displaystyle \iint_{\Omega}\left[F_{3}\right ]_{z = f_{1}(x,y)}^{f_{2}(x,y)}dydx$](img4645.png) |
||
 |
![$\displaystyle \iint_{\Omega}[F_{3}(x,y,f_{2}(x,y)) - F_{3}(x,y,f_{1}(x,y)) ]dy dx$](img4646.png) |
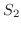 において,曲線座標
において,曲線座標 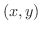 に対する法線単位ベクトル
に対する法線単位ベクトル
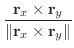
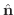 と一致しているが,曲面
と一致しているが,曲面  では法線単位ベクトルは
では法線単位ベクトルは
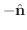 に等しい.よって
に等しい.よって
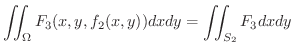
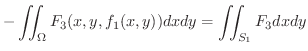
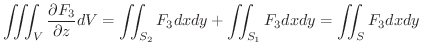
 を他の平面に正射影することにより
を他の平面に正射影することにより
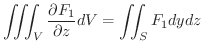
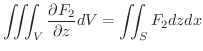
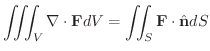
領域  が一般な場合には,平面におけるGreenの定理の証明のように,
が一般な場合には,平面におけるGreenの定理の証明のように, 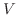 を部分領域に分割して証明すればよい.
を部分領域に分割して証明すればよい.

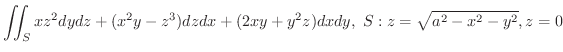
解
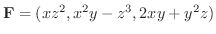 よりdivFを求めると
よりdivFを求めると
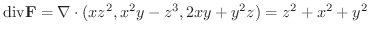
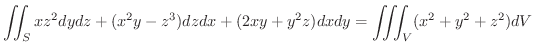
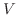 は半径
は半径  の上半球より球面座標変換
の上半球より球面座標変換
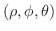 を用いると
を用いると
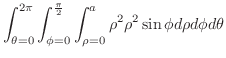 |
 |
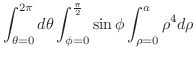 |
|
 |
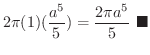 |
(a)
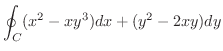 , ただし,
, ただし,  は点
は点
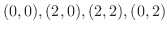 を頂点とする正方形.
を頂点とする正方形.
(b)
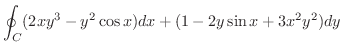 , ただし,
, ただし,  は点
は点  から点
から点
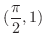 を放物線
を放物線
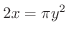 に沿って進む.
に沿って進む.
(c)
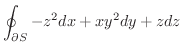 , ただし,
, ただし,
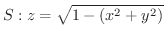
(a)
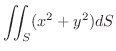 , ただし,
, ただし,
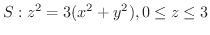
(b)
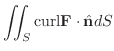 , ただし,
, ただし,
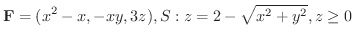
(c)
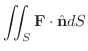 ,
ただし,
,
ただし,
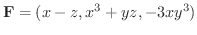 ,
,
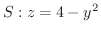 ,
,
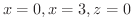
(d)
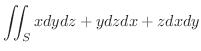 ,
ただし,
,
ただし,  は 円柱
は 円柱
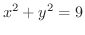 と平面
と平面
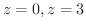 で囲まれた領域
で囲まれた領域
 で囲まれた領域の面積
で囲まれた領域の面積 は,
は,
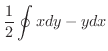 で与えられることを示そう.
で与えられることを示そう.
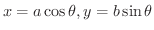 の面積を求めよう.
の面積を求めよう.
 をスカラー場とするとき次の式が成り立つことを示そう.
をスカラー場とするとき次の式が成り立つことを示そう.
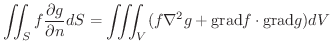 ここで
ここで
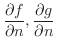 はそれぞれ
はそれぞれ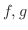 の
の  における外向き法線方向の方向微分係数を表わす.
における外向き法線方向の方向微分係数を表わす.