Next: ベクトル積分定理(integral theorems of vector Up: ベクトル解析(VECTOR ANALYSIS) Previous: 線積分(line integrals) 目次 索引
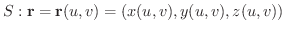 上の任意の点
上の任意の点
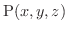 に対して定義されたスカラー場を
に対して定義されたスカラー場を
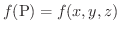 とします.ただし,曲面
とします.ただし,曲面  は滑らかな曲面とします.
は滑らかな曲面とします.
 を
を  個の小さな面
個の小さな面
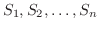 に分割し,この分割を
に分割し,この分割を 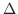 で表わします.次に曲面
で表わします.次に曲面 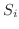 の面積を
の面積を
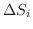 とし,
とし, 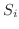 の中に点
の中に点
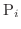 をとり,次の和を考えます.
をとり,次の和を考えます.
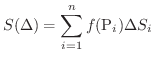
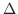 を限りなく小さくしたとき,
を限りなく小さくしたとき,  が限りなく
が限りなく に近づくならば,この極限値
に近づくならば,この極限値  をスカラー場
をスカラー場  の 面積分(surface integral) といい
の 面積分(surface integral) といい
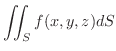
で表わします.
ここで面積素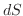 は
は
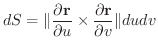
 の曲面
の曲面  上での面積分は,次のように表わされます.
上での面積分は,次のように表わされます.
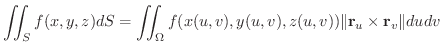
ここで,  は
は  に対応する
に対応する 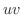 平面上の領域です.
平面上の領域です.
 の放物面
の放物面
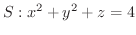 のうち
のうち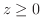 の部分上での面積分を求めてみましょう.
の部分上での面積分を求めてみましょう.
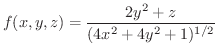
解
曲面
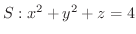 より対応する
より対応する 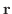 を位置ベクトルとすると
を位置ベクトルとすると
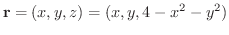
 の法線ベクトル
の法線ベクトル
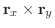 を求めると
を求めると
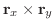 |
 |
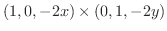 |
|
 |
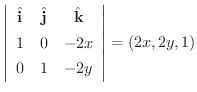 |
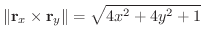
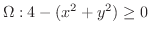 より極座標変換を行なうと
より極座標変換を行なうと
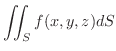 |
 |
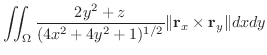 |
|
 |
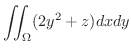 |
||
 |
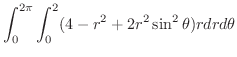 |
||
 |
![$\displaystyle \int_{0}^{2 \pi}\left[2r^2 - \frac{r^2}{4} + \frac{r^4}{2}\sin^{2}\theta \right ]_{0}^{2 \pi} d\theta$](img4492.png) |
||
 |
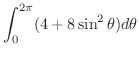 |
||
 |
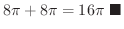 |
線積分と同様に曲面  上で定義されたベクトル場
上で定義されたベクトル場
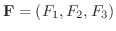 の面積分を曲面
の面積分を曲面  の法線ベクトル
の法線ベクトル
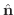 を用いて定義し,次のように表わします.
を用いて定義し,次のように表わします.
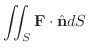
なお
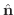 の方向と
の方向と
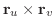 の方向は等しいので
の方向は等しいので
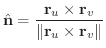
 上のベクトル場
上のベクトル場  の面積分は次のように2重積分で表わされます.
の面積分は次のように2重積分で表わされます.
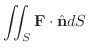 |
 |
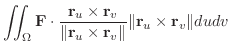 |
|
 |
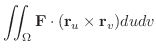 |
||
 |
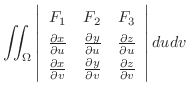 |
また,
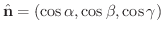 とすると,次のようにも書けます.
とすると,次のようにも書けます.
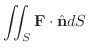 |
 |
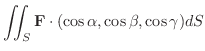 |
|
 |
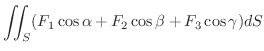 |
||
 |
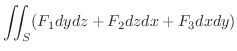 |
ここで,ベクトル場Fを,流体が流管中を定常的にながれるときの,ある点での速度場とするとき,
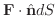 を
を  の
の
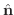 に向かう束(flux) といいます.よって速度場
に向かう束(flux) といいます.よって速度場  の束が流速(流量)
の束が流速(流量)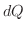 となり,その面積分
となり,その面積分
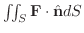 を 束積分(flux integral) といい,全流束を表わします.
を 束積分(flux integral) といい,全流束を表わします.
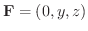 ,曲面
,曲面
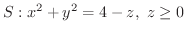 において
において
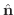 は内側から外側へ向かう法線ベクトルとする.このとき面積分
は内側から外側へ向かう法線ベクトルとする.このとき面積分
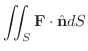 を求めてみましょう.
を求めてみましょう.
解
位置ベクトルは
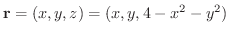 より
より
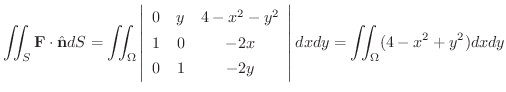
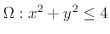 より極座標変換を行うと
より極座標変換を行うと
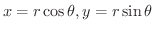 より
より
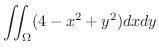 |
 |
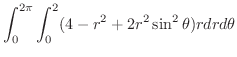 |
|
 |
![$\displaystyle \int_{0}^{2 \pi} \left[2r^2 - \frac{r^2}{4} + \frac{r^4}{2}\sin^{2}\theta \right ]_{0}^{2} d\theta$](img4515.png) |
||
 |
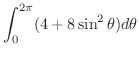 |
||
 |
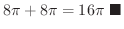 |