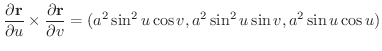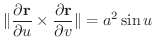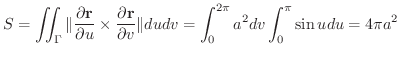Next: スカラー場とベクトル場(scalar field and vector Up: ベクトル解析(VECTOR ANALYSIS) Previous: ベクトル解析(VECTOR ANALYSIS) 目次 索引
 平面上の有界閉領域
平面上の有界閉領域  上で定義された関数
上で定義された関数
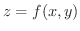 が
が 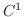 級であるとき,
級であるとき,
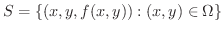
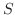 上の点Pの位置ベクトル
上の点Pの位置ベクトル
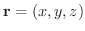 が2変数
が2変数 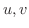 の関数であるとき,
の関数であるとき,
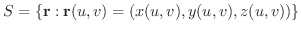
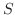 のパラメター表示といいます.
のパラメター表示といいます.
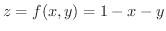 をパラメーター表示せよ.
をパラメーター表示せよ.
解
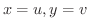 とすると,
とすると, 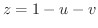 よって
よって
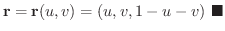
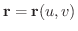 において
において 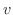 を固定して
を固定して 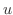 だけ変化させると,
だけ変化させると,
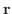 は曲面
は曲面 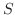 上で 1 つの曲線を描きます.この曲線を
上で 1 つの曲線を描きます.この曲線を 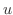 曲線(u-curve)
といいます.同様に
曲線(u-curve)
といいます.同様に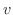 曲線(v-curve)も定義されます.また,
曲線(v-curve)も定義されます.また,
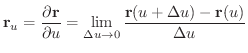
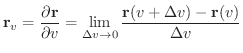
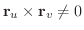 のとき,パラメター表示された曲面
のとき,パラメター表示された曲面
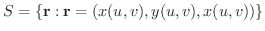 は滑らかな曲面になります.
は滑らかな曲面になります.
曲面
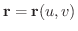 上の点
上の点
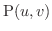 において,その点を通り,
2 つのベクトル
において,その点を通り,
2 つのベクトル
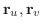 によって決定される平面を,
点
によって決定される平面を,
点  における曲面の 接平面(tangent plane) といいます.
また接平面に垂直なベクトル
における曲面の 接平面(tangent plane) といいます.
また接平面に垂直なベクトル
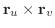 を
法線ベクトル(normal vector) といいます.図8.1参照.
を
法線ベクトル(normal vector) といいます.図8.1参照.
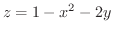 の点
の点 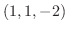 における接平面を求めてみましょう.
における接平面を求めてみましょう.
解
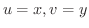 とすると,
とすると,
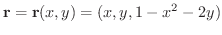
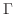 の法線ベクトル
の法線ベクトル
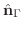 を求めると
を求めると
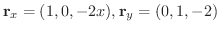
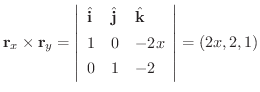
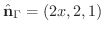 よって点
よって点 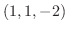 における接平面の方程式は
における接平面の方程式は
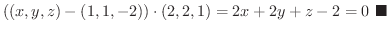
空間の点Pの位置ベクトルが, 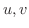 の関数
の関数 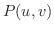 で与えられ,
で与えられ, 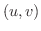 が
が 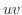 平面の領域
平面の領域  を動くとき,点Pは空間内に1つの曲面を描きます.このとき点Pが描く曲面の面積
を動くとき,点Pは空間内に1つの曲面を描きます.このとき点Pが描く曲面の面積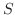 は2重積分の応用として
は2重積分の応用として
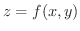 であたえられる曲面の面積を求めたときと同じようにして
であたえられる曲面の面積を求めたときと同じようにして
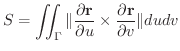
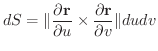
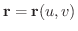 の 面積素(area element) といいます.
の 面積素(area element) といいます.
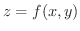 であたえられているとき,面積素を求めて,曲面積の公式を導いてみましょう.
であたえられているとき,面積素を求めて,曲面積の公式を導いてみましょう.
解
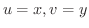 とおくと,
とおくと,
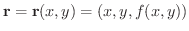
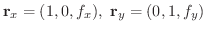
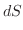 |
 |
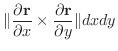 |
|
 |
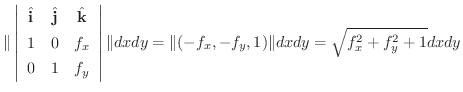 |
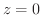 であたえられる平面を
であたえられる平面を  とすると,
とすると,
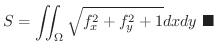
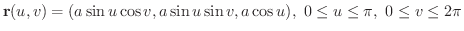 で与えられている.これを用いて球の表面積を求めてみましょう.
で与えられている.これを用いて球の表面積を求めてみましょう.
解
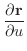 |
 |
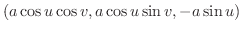 |
|
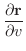 |
 |
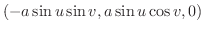 |