Next: 交項級数(alternating series) Up: 級数(SERIES) Previous: 級数の定義(definition of series) 目次 索引
前節で見たように,級数の収束や発散を支配するのは,項の番号 が大きくなってからです.そこで,
が大きくなってからです.そこで,
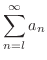 と表す代わりに,
と表す代わりに,
 と表すことにします.
と表すことにします.
すべての項が正である級数を 正項級数(nonnegative term series) といいます.第n部分和を 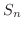 とすれば,
とすれば, 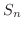 は単調増加であり,
は単調増加であり,
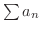 は収束するか
は収束するか
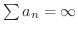 かのどちらかです.したがって,
かのどちらかです.したがって,
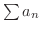 が収束するのと
が収束するのと
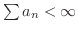 とは同等であることがわかります.先に示した無限等比級数と一般調和級数は正項級数の代表的な例です.
とは同等であることがわかります.先に示した無限等比級数と一般調和級数は正項級数の代表的な例です.
さて級数の収束,発散を調べるのに,よく性質のわかっている別の級数と比較して調べることがあります.
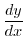 つの正項級数
つの正項級数
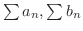 において,
有限な極限値
において,
有限な極限値
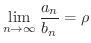
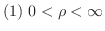 ならば,
ならば,
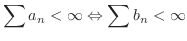
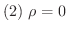 ならば,
ならば,
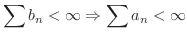
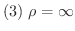 ならば,
ならば,
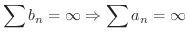
証明
(1)
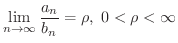 より
より 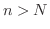 ならば,
ならば,
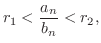
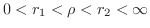 となる整数
となる整数 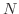 が存在する.よって
が存在する.よって
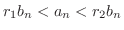 .これより
.これより
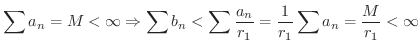
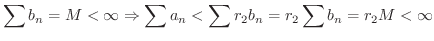
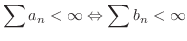

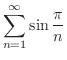
解
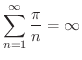 と比較します.
と比較します.
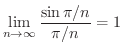
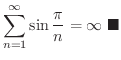
 を区間
を区間
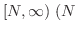 は自然数
は自然数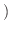 で連続な狭義の単調減少関数で,
で連続な狭義の単調減少関数で,
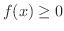 であるとする.このとき
であるとする.このとき
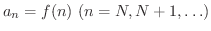
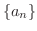 に対して
に対して
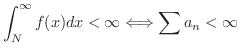
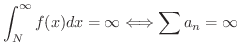
証明
 は
は 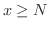 で狭義の単調減少関数であるから,
で狭義の単調減少関数であるから, 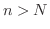 に対しては
に対しては
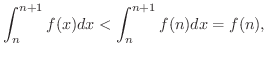
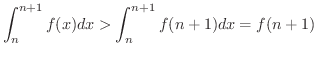
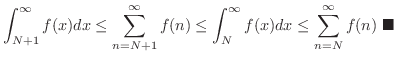
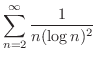
解
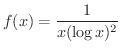 とおくと
とおくと
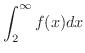 |
 |
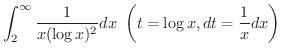 |
|
 |
![$\displaystyle \int_{\log{2}}^{\infty}\frac{1}{t^{2}}dt = \left[-\frac{1}{t}\right ]_{\log{2}}^{\infty-0} = \frac{1}{\log{2}} < \infty$](img2773.png) |
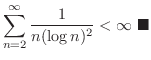
次に,フランスの数学者 Jean le Rond d'Alembert (1717-1783) によって示された正項級数が収束するための十分条件について学びます.
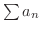 において
において
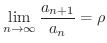
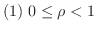 ならば,
ならば,
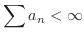
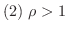 ならば,
ならば,
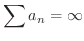
証明
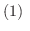 の証明.
の証明.
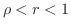 であるような
であるような 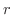 をとり,この
をとり,この 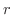 に対して適当な自然数
に対して適当な自然数 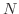 をとると,
をとると, 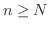 であるすべての自然数
であるすべての自然数  に対して,
に対して,
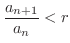
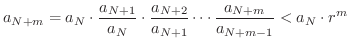
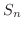 は
は
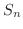 |
 |
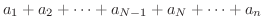 |
|
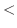 |
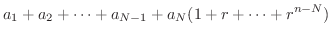 |
||
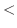 |
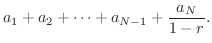 |
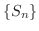 は上に有界な単調増加数列となり収束します.
は上に有界な単調増加数列となり収束します.
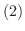 の証明は各自試みて下さい.
の証明は各自試みて下さい.

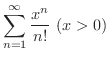
解