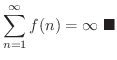Next: 正項級数(nonnegative term series) Up: 級数(SERIES) Previous: 級数(SERIES) 目次 索引
深さ 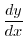 m の井戸にカエルが落ちました.カエルは必死に井戸からでようとしています.一回目のジャンプで1mとびあがり,二回目のジャンプで
m の井戸にカエルが落ちました.カエルは必死に井戸からでようとしています.一回目のジャンプで1mとびあがり,二回目のジャンプで
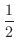 m, 三回目のジャンプで
m, 三回目のジャンプで
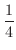 m と次々に前回の半分の距離をジャンプしていきました.ここで質問です.このカエルはやがて外にでれたでしょうか.考えてみましょう.まず,
m と次々に前回の半分の距離をジャンプしていきました.ここで質問です.このカエルはやがて外にでれたでしょうか.考えてみましょう.まず,
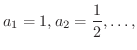 とおくと, 質問は
とおくと, 質問は
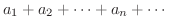
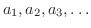 が数列のとき,この数列を用いて新たに数列
が数列のとき,この数列を用いて新たに数列
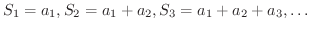
 項までの部分和
項までの部分和 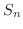 を 第
を 第 部分和(nth partial sum) といいます.
部分和(nth partial sum) といいます.
数列
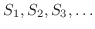 は形式的に
は形式的に
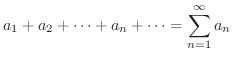
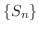 が収束するとき,つまり
が収束するとき,つまり
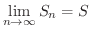
 が存在するとき,級数
が存在するとき,級数
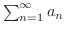 は
は  に収束する(convergent) といい,
に収束する(convergent) といい,
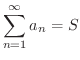
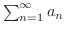 の和は
の和は  であるといいます.また,数列
であるといいます.また,数列 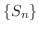 が収束しないとき,級数
が収束しないとき,級数
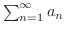 は 発散する(divergent) といいます.
は 発散する(divergent) といいます.
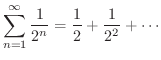 を求めてみましょう.
を求めてみましょう.
解
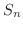 |
 |
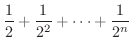 |
|
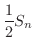 |
 |
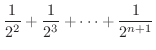 |
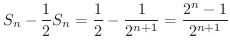
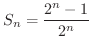
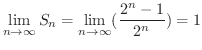
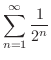 は収束し,その和は
は収束し,その和は 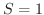 です.
です.

これを一般化したものに次の定理があります.次の級数は簡単に収束,発散の判定ができるのでよく用いられます.
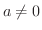 のとき,
のとき,
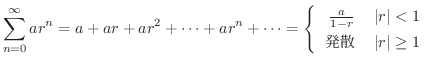
証明
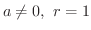 のとき,
のとき,
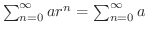 より発散.よって
より発散.よって 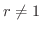 について考えます.
について考えます.
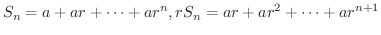
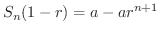
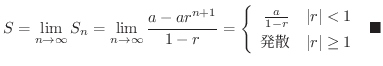
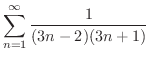 を求めてみましょう.
を求めてみましょう.
解
まず
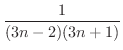 を部分分数で書き直してみると,
を部分分数で書き直してみると,
![$\displaystyle \frac{1}{(3n-2)(3n+1)} = \frac{1}{3}[\frac{1}{3n-2} - \frac{1}{3n+1}] $](img2695.png)
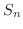 を求めると
を求めると
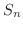 |
 |
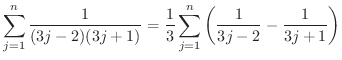 |
|
 |
![$\displaystyle \frac{1}{3}[1 - \frac{1}{4} + \frac{1}{4} - \cdots - \frac{1}{3n-2} + \frac{1}{3n-2} - \frac{1}{3n+1} ]$](img2697.png) |
||
 |
![$\displaystyle \frac{1}{3}[1 - \frac{1}{3n+1}]$](img2698.png) |
![$\displaystyle S = \lim_{n \rightarrow \infty} S_{n} = \lim_{n \rightarrow \infty}\frac{1}{3}[1 - \frac{1}{3n+1}] = \frac{1}{3}
\ensuremath{\ \blacksquare}
$](img2699.png)
 部分和は途中がすべて消えてしまうので,telescoping sum(望遠鏡級数)ともよばれています.
ここで収束する級数すべてにおいて成り立つ定理を示します.
部分和は途中がすべて消えてしまうので,telescoping sum(望遠鏡級数)ともよばれています.
ここで収束する級数すべてにおいて成り立つ定理を示します.
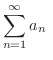 が収束するならば,
が収束するならば,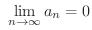
証明
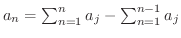 よって
よって
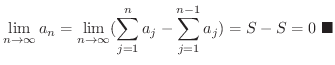
この定理の対偶をとると数列 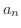 が収束しなければ,級数
が収束しなければ,級数
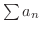 は発散することになります.これより,級数の収束,発散を調べるときには,この定理をまず用いてみて下さい.
は発散することになります.これより,級数の収束,発散を調べるときには,この定理をまず用いてみて下さい.
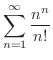 の収束,発散について調べてみましょう.
の収束,発散について調べてみましょう.
解
まず,
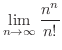 を計算してみましょう.
を計算してみましょう.
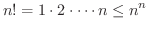
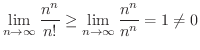
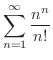 は発散します.
は発散します.
この定理の逆は必ずしも正しくありません.例えば級数
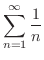
 は0に収束しますが,この級数は次に示すように調和級数なので発散します.
は0に収束しますが,この級数は次に示すように調和級数なので発散します.
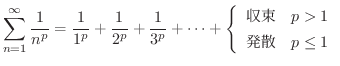
証明
まず,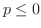 のとき,
のとき,
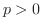 の場合を考えます.
の場合を考えます.
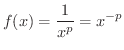 とおくと,
とおくと,
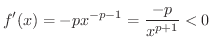
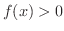 は
は
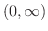 で単調減少となるので,
で単調減少となるので,
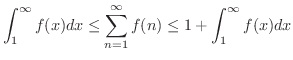
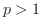 の場合を考えてみましょう.
の場合を考えてみましょう.
![$\displaystyle \int_{1}^{\infty}f(x)dx = \int_{1}^{\infty}\frac{1}{x^p} dx = \left[\frac{x^{-p+1}}{-p+1}\right]_{1}^{\infty-0} = \frac{1}{p-1} < \infty $](img2718.png)
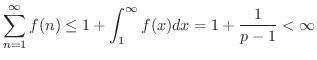
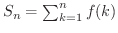 は上に有界な単調増加数列となるので収束.
また
は上に有界な単調増加数列となるので収束.
また 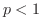 の場合
の場合
![$\displaystyle \int_{1}^{\infty}f(x)dx = \int_{1}^{\infty}\frac{1}{x^p} dx = \left[\frac{x^{-p+1}}{-p+1}\right]_{1}^{\infty-0} = \infty $](img2722.png)
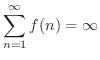
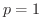 の場合
の場合
![$\displaystyle \int_{1}^{\infty}f(x)dx = \int_{1}^{\infty}\frac{1}{x} dx = \left[\log{x}\right]_{1}^{\infty-0} = \infty $](img2724.png)