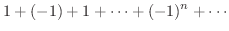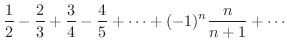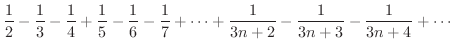Next: *関数項級数(series of functions) Up: 級数(SERIES) Previous: 正項級数(nonnegative term series) 目次 索引
正の項と負の項が交互にあらわれる級数を 交項級数(alternating series) といいます.
ここで,ドイツの数学者 Gottfried Wilhelm Leibniz (1646-1716) によって示された交項級数が収束するための十分条件を学びます.
 つの条件が満たされれば,交項級数
つの条件が満たされれば,交項級数
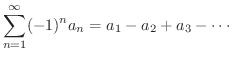
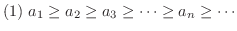
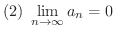
証明
この級数の第n部分和を 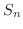 とすると,
とすると,
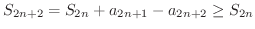
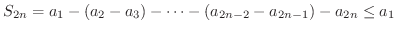
 は上に有界な単調増加数列となるので収束します.ここで,
は上に有界な単調増加数列となるので収束します.ここで,
 とすると,
とすると,
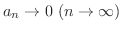 より
より
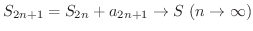
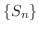 は
は  に収束します.したがって
に収束します.したがって
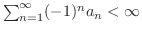

交項級数
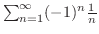 はLeibnizの定理の条件を満たしているので収束します.ところがこの級数の各項の絶対値をとって作った級数
はLeibnizの定理の条件を満たしているので収束します.ところがこの級数の各項の絶対値をとって作った級数
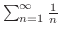 は調和級数となり発散します.このように
は調和級数となり発散します.このように
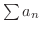 が収束し
が収束し
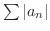 が発散する級数を 条件収束(conditionally convergent) するといいます.また
が発散する級数を 条件収束(conditionally convergent) するといいます.また
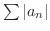 も収束する級数
も収束する級数
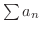 を 絶対収束(absolute convergent) するといいます.
を 絶対収束(absolute convergent) するといいます.
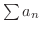 が収束しても
が収束しても
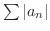 は収束しない場合があることは分かりました.では,その逆はどうなのでしょうか.つまり,
は収束しない場合があることは分かりました.では,その逆はどうなのでしょうか.つまり,
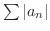 が収束して
が収束して
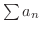 が収束しない場合はあるのでしょうか.ちょっと考えてみて下さい.
が収束しない場合はあるのでしょうか.ちょっと考えてみて下さい.
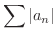 が収束すれば,
が収束すれば,
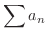 も収束する.
も収束する.
証明
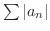 の第n部分和を
の第n部分和を 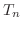 ,
,
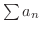 の第n部分和を
の第n部分和を 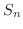 とおくと,
とおくと,
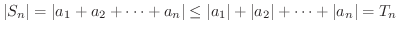
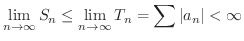
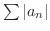 が収束すれば,
が収束すれば,
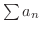 も収束します.
も収束します.
ここで,収束する級数と発散する級数の決定的な違いを調べてみましょう.まず,次のような交項級数を考えます.
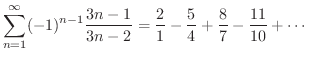
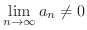 となるので発散条件より発散します.この級数を隣り合った2つの項をかっこでくくって作った級数
となるので発散条件より発散します.この級数を隣り合った2つの項をかっこでくくって作った級数
 |
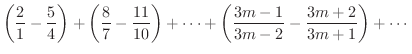 |
||
 |
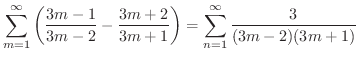 |
 |
 |
||
 |
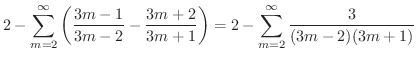 |
||
 |
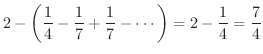 |