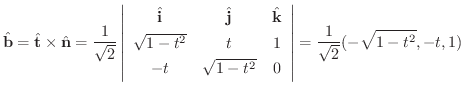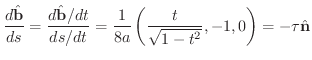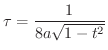Next: 偏微分法(PARTIAL DIFFERENTIATION) Up: ベクトル関数(VECTOR FUNCTIONS) Previous: 曲線(space curves) 目次 索引
曲線
![$\displaystyle C : {\bf r}(t) = (x(t), y(t), z(t)), \ t \in [a,b] $](img3138.png)
![$[a,b]$](img158.png) は時間の区間と考え,
は時間の区間と考え,
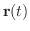 を時間
を時間  における物体の位置と考えます.すると
運動
における物体の位置と考えます.すると
運動
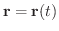 に対して,
に対して,
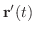 は運動の 速度ベクトル(velocity).また,
は運動の 速度ベクトル(velocity).また,
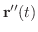 は 加速度ベクトル(acceleration) となり,それぞれ
は 加速度ベクトル(acceleration) となり,それぞれ
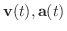 で表わします.つまり,
で表わします.つまり,
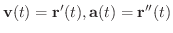
すでに学んだように,接線単位ベクトルは
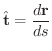 で表わせるので,速度ベクトルは
で表わせるので,速度ベクトルは
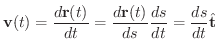
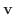 の大きさ,
の大きさ,
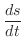 は弧の長さの変化率または速さで
は弧の長さの変化率または速さで 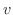 で表わされます.つまり,
で表わされます.つまり,
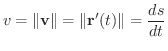
次に加速度についてもう少しよく理解するために,速度ベクトルを考えてみましょう.
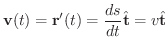
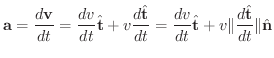
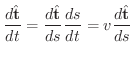
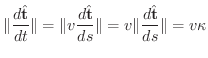
 |
 |
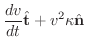 |
|
 |
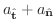 |
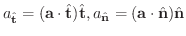
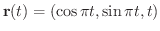
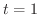 のとき
のとき
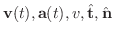 を求めてみましょう.
を求めてみましょう.
解
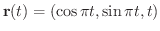
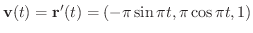
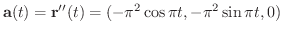
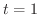 のとき
のとき
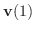 |
 |
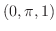 |
|
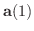 |
 |
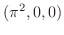 |
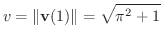
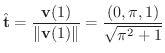
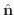 を求めるには色々な方法があります.ここでは計算が簡単な方法を考えます.
を求めるには色々な方法があります.ここでは計算が簡単な方法を考えます.
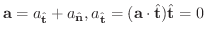
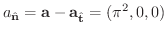
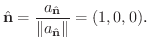
他にも
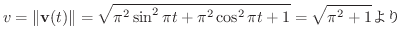
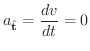
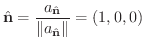 と求めることができます.
と求めることができます.

接線単位ベクトル
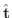 ,主法線ベクトル
,主法線ベクトル
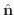 と直交するベクトル
と直交するベクトル
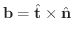
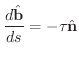
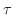 をねじれ率(torsion)といいます.
をねじれ率(torsion)といいます.
ここで,これまでにでてきた3つの単位ベクトル
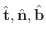 について調べてみましょう.図5.2参照.
について調べてみましょう.図5.2参照.
まず,
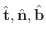 は互いに直交するベクトルです.また,これらのベクトルの間には Frenet-Serret (1819-1885) によって示された次の関係が成り立ちます.
は互いに直交するベクトルです.また,これらのベクトルの間には Frenet-Serret (1819-1885) によって示された次の関係が成り立ちます.
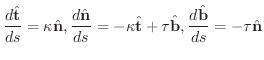
証明
式5.1 より
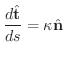 また,ねじれ率の定義より
また,ねじれ率の定義より
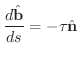 .次に.
.次に.
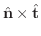 を
を 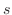 で微分すると
で微分すると
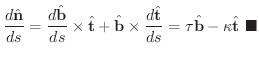
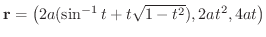 について,次のものを求めよう. ただし,
について,次のものを求めよう. ただし,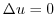 は任意の正の定数とする.
は任意の正の定数とする.
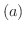
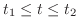 に対する弧長
に対する弧長
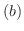 接線単位ベクトル
接線単位ベクトル
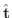
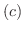 主法線単位ベクトル
主法線単位ベクトル
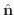 と 曲率
と 曲率 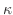
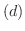 従法線単位ベクトル
従法線単位ベクトル
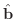 とねじれ率
とねじれ率 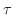
解
(a)
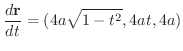 より
より
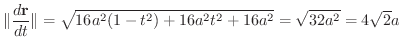
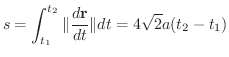
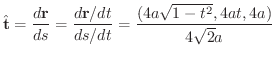
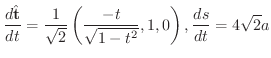 より
より
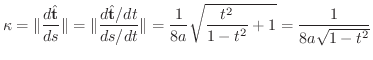
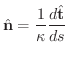 より
より
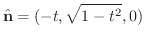
(d)