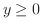Next: 点の運動(motion of objects) Up: ベクトル関数(VECTOR FUNCTIONS) Previous: ベクトル関数(vector functions) 目次 索引
空間の点P 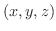 の描く空間曲線は
の描く空間曲線は
![$\displaystyle C = \{(x,y,z) : x = x(t), y = y(t), z = z(t), t \in [a,b] \} $](img3025.png)
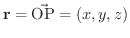 が
が 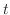 のベクトル関数として
のベクトル関数として
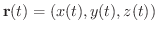
次に,ベクトル関数
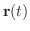 の導関数
の導関数
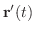 は幾何学的に何を表しているのか考えてみましょう.
は幾何学的に何を表しているのか考えてみましょう.
ベクトル関数
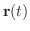 の導関数
の導関数
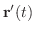 は
は
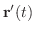 の定義より
の定義より
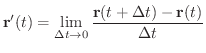
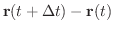 は
は
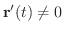 ならば,たとえ
ならば,たとえ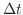 が0に近づいても
が0に近づいても 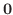 にならず,接線の方向ベクトルに近づいていくことが分かります.よってこの極限値
にならず,接線の方向ベクトルに近づいていくことが分かります.よってこの極限値
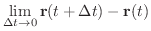
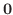 となり,
となり, 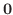 には方向がありません.
には方向がありません.
そこで,これを回避するために 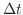 が小さいときに,大きな長さを得られるような次のベクトルを考えます.
が小さいときに,大きな長さを得られるような次のベクトルを考えます.
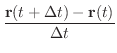
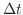 が0でないとき
が0でないとき
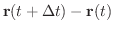 と平行です.つまり,このベクトルは接線の方向ベクトルと平行です.よってこの極限値
と平行です.つまり,このベクトルは接線の方向ベクトルと平行です.よってこの極限値
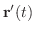 が存在するとき,この極限値を接線の方向ベクトルと考えることができるので,
が存在するとき,この極限値を接線の方向ベクトルと考えることができるので,
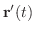 を曲線
を曲線
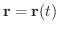 の 接線ベクトル(tangent vector) といいます.
また
の 接線ベクトル(tangent vector) といいます.
また
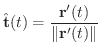
ここで
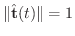 に注意すると,例題5.1より
に注意すると,例題5.1より
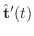 と
と
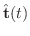 は直交します.そこで
は直交します.そこで
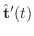 を曲線
を曲線
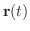 の 法線ベクトル(normal vector) といいます.また,
の 法線ベクトル(normal vector) といいます.また,
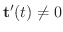 のとき,
のとき,
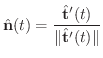
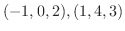 を通る直線の方程式を求めてみましょう.
を通る直線の方程式を求めてみましょう.
解
求める直線は始点を 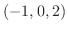 にもち,方向が
にもち,方向が
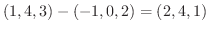 と考えられるので,直線上の任意の点を
と考えられるので,直線上の任意の点を 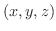 とすると,
とすると,
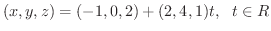
 について解くと
について解くと
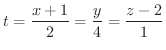

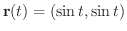 を描いてみましょう.
を描いてみましょう.
解
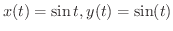 より
より 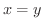 .ここで注意しなければならないのは,
.ここで注意しなければならないのは, 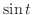 のとる値は
のとる値は 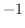 から
から 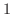 なので,求める曲線は
なので,求める曲線は
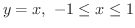 となります.
となります.

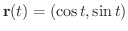 の
の
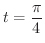 における接線の方程式を求めてみましょう.
における接線の方程式を求めてみましょう.
解 接線ベクトルは
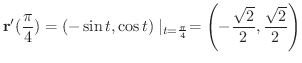
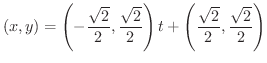
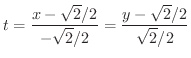

曲線
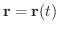 が
が
![${\bf r}^{\prime}(t) \neq 0, {\bf r}^{\prime}(t) \in C[a,b]$](img3062.png) のとき,曲線 r を 滑らかな曲線(smooth curve) といいます.滑らかな曲線
のとき,曲線 r を 滑らかな曲線(smooth curve) といいます.滑らかな曲線
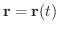 の
の
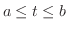 の部分の長さを 弧長(arc length) といい,
の部分の長さを 弧長(arc length) といい, 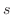 で表わします.では,弧長
で表わします.では,弧長 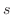 はどうやったら求まるか考えてみましょう.
はどうやったら求まるか考えてみましょう.
区間 ![$[a,b]$](img158.png) 内の微小区間
内の微小区間
![$[t, t+\Delta t]$](img3064.png) に対応する曲線
に対応する曲線
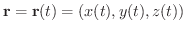 の弧 PQ の長さは線分 PQ で近似されると考えられます.このとき,
の弧 PQ の長さは線分 PQ で近似されると考えられます.このとき,
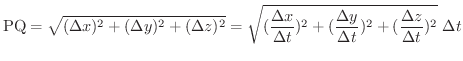
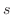 は定積分
は定積分
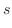 |
 |
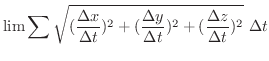 |
|
 |
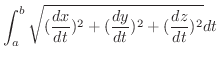 |
||
 |
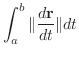 |
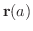 から
から
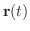 までの弧長
までの弧長 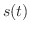 は
は
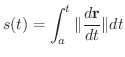
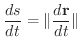
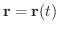 が滑らかな曲線のとき,
が滑らかな曲線のとき,
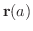 から
から
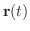 までの弧長
までの弧長 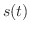 は
は
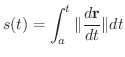
ここで気づいたと思いますが,  を時間と考えると,
を時間と考えると,
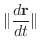 は微小時間内での位置の変化と考えられるので,点Pの動く速さを表わします.よって,曲線の長さ
は微小時間内での位置の変化と考えられるので,点Pの動く速さを表わします.よって,曲線の長さ 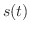 は点Pが時間
は点Pが時間 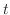 内に動いた距離と考えることができます.
内に動いた距離と考えることができます.
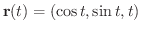 の
の
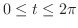 の部分の長さを求めてみましょう.
の部分の長さを求めてみましょう.
解
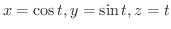 より,
より,
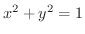 となり,
となり,
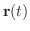 は半径1の円柱の回りをらせん状に回転する滑らかな曲線だということが分かります.そこで
は半径1の円柱の回りをらせん状に回転する滑らかな曲線だということが分かります.そこで
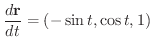
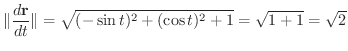
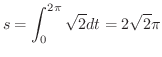

 をパラメターとして曲線
をパラメターとして曲線
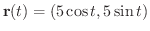 を表わしてみましょう.
を表わしてみましょう.
解
曲線
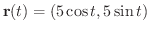 より
より
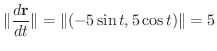
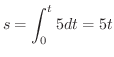
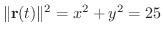 より曲線
より曲線
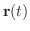 は原点を中心とする半径5の円です.よって弧長sは
は原点を中心とする半径5の円です.よって弧長sは 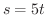 .これより
.これより
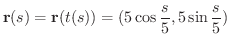

曲線  が弧長sをパラメターとして
が弧長sをパラメターとして
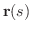 で表わされているとき,接線ベクトルを求めると
で表わされているとき,接線ベクトルを求めると
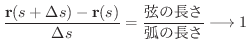
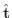 は
は
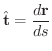
でも表わせます.
ここで曲線の曲がり具合について考えてみましょう.まず平面上の曲線について考えてみましょう.曲線上の点Pでの接線 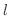 と
と  軸とが作る角度を
軸とが作る角度を 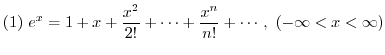 とします.点Pが動くに従って接線
とします.点Pが動くに従って接線 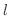 と
と 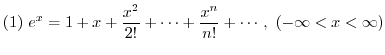 は変化します.このとき,単位弧長あたりの
は変化します.このとき,単位弧長あたりの 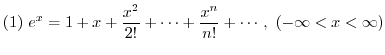 の変化率を 曲率(curvature) といい
の変化率を 曲率(curvature) といい
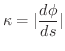
で表わします.
ここで接線単位ベクトル
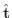 は
は
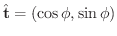 で表わすことができます.よって単位弧長あたりの接線ベクトルの変化率を調べると
で表わすことができます.よって単位弧長あたりの接線ベクトルの変化率を調べると
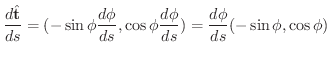
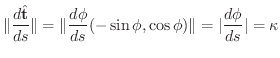
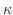 は,単位弧長あたりの接線ベクトルの変化率でも表わすことができます.
は,単位弧長あたりの接線ベクトルの変化率でも表わすことができます.
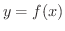 の曲率を求めてみましょう.
の曲率を求めてみましょう.
解
まず,
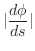 を求めてみましょう.
を求めてみましょう.
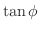 は接線の傾きなので,
は接線の傾きなので,
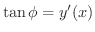 となります.よって
となります.よって
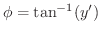
 について微分すると
について微分すると
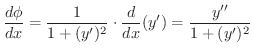
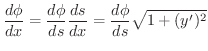
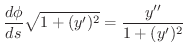
![$\displaystyle \kappa = \vert\frac{d \phi}{ds}\vert = \frac{\vert y^{\prime\prime}\vert}{[1 + (y^{\prime})^2]^{3/2}} $](img3107.png)
となります.

空間の曲線の曲率は
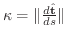 を定義として使います.すると,
を定義として使います.すると,
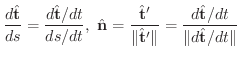
(a) 点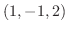 を通りベクトル
を通りベクトル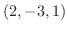 に平行.
に平行.
(b) 点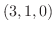 を通り線分
を通り線分
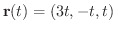 に平行.
に平行.
(c) 点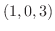 と
と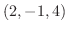 を通る.
を通る.
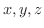 の方程式で表わそう.
の方程式で表わそう.
(a)
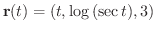 ただし,
ただし,
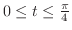
(b)
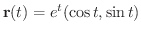 ただし,
ただし,
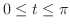
(c)
 ただし,
ただし,