Next: 曲線(space curves) Up: ベクトル関数(VECTOR FUNCTIONS) Previous: ベクトル関数(VECTOR FUNCTIONS) 目次 索引
実数 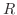 の部分集合
の部分集合  に属する各点
に属する各点  に対して,実関数
に対して,実関数
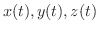 が与えられるとき,1つのベクトル
が与えられるとき,1つのベクトル
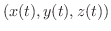 を考えることができます.このベクトル
を考えることができます.このベクトル
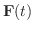 を
を  から
から 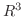 への1変数ベクトル値関数(vector-valued function)または ベクトル関数(vector function) といい,
への1変数ベクトル値関数(vector-valued function)または ベクトル関数(vector function) といい,
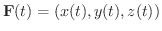
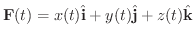
しばしば
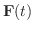 は幾何学的に実軸
は幾何学的に実軸  から原点と点
から原点と点
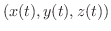 を結ぶベクトルへの写像として扱われます.
を結ぶベクトルへの写像として扱われます.
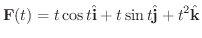 のとき,
のとき,
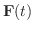 の軌跡を求めてみましょう.
の軌跡を求めてみましょう.
解
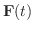 の成分は
の成分は
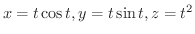 であるから,
であるから,
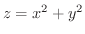 となり,
となり,
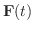 の軌跡
の軌跡
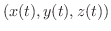 は放物面
は放物面
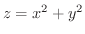 上にあることが分かります.
上にあることが分かります.

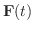 において,
において,
 のとき,
のとき,
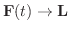 ならば,
ならば,
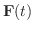 の極限値は
の極限値は 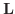 であるといい,次のように表わす.
であるといい,次のように表わす.
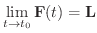
極限値の定義は1変数関数のときと同じなので,たぶん連続性の定義も1変数関数のときと同じになると期待するでしょう.実際そのとうりです.
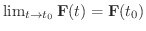 が成り立つとき,ベクトル関数
が成り立つとき,ベクトル関数
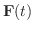 は
は 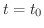 で連続であるという.また,区間
で連続であるという.また,区間 ![$[a,b]$](img158.png) のすべての
のすべての  で連続なとき,
で連続なとき,
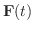 は区間
は区間 ![$[a,b]$](img158.png) で連続であるといい,
で連続であるといい,
![${\bf F}(t) \in C[a,b]$](img2980.png) と表わす.
と表わす.
このように1変数関数における様々な定義はベクトル関数へと継承されます.
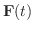 は
は 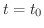 において,
において,
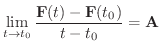
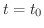 で微分可能(differentiable)
であるという.また,この極限値
で微分可能(differentiable)
であるという.また,この極限値 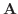 を点
を点 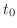 における微分係数といい,
における微分係数といい,
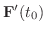 で表わす.
で表わす.
次の節で学びますがベクトル
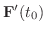 の方向は,
の方向は,
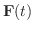 によって描かれる曲線の
によって描かれる曲線の 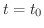 での接線方向になります.図5.1参照
での接線方向になります.図5.1参照
ベクトルの和やスカラー倍がそれぞれの対応する成分の和やスカラー倍で定義されたように,ベクトル関数の極限値,微分係数,不定積分の計算は,ベクトル関数の成分の極限値,微分係数,不定積分より求めることができます.
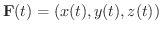 とすると,次のことが成り立つ.
とすると,次のことが成り立つ.
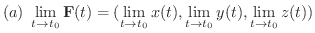
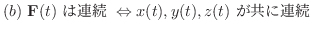
![$\displaystyle{(c) \ {\bf F} \in C'[a,b] \Rightarrow {\bf F}^{\prime}(t_{0}) = (x^{\prime}(t_{0}),y^{\prime}(t_{0}),z^{\prime}(t_{0}))}$](img2988.png)
![$\displaystyle{(d) \ {\bf F} \in C[a,b] \Rightarrow \int_{a}^{b}{\bf F}(t) dt = (\int_{a}^{b} x(t)dt, \int_{a}^{b} y(t)dt, \int_{a}^{b} z(t)dt)}$](img2989.png)
証明
(a)
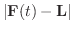 |
 |
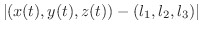 |
|
 |
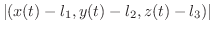 |
||
 |
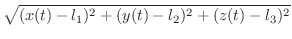 |
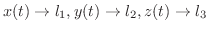 ならば,
ならば,
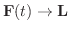 .また,
.また,
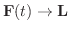 ならば,
ならば,
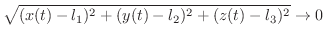
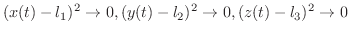
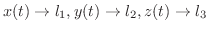 より,
より,
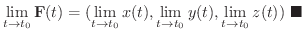
(b),(c),(d)の証明は演習問題にまわします.
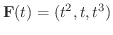 のとき,
のとき,
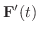 を求めてみましょう.
を求めてみましょう.
解 それぞれの成分を微分することにより
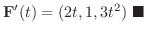
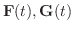 が
が  について微分可能なベクトル関数ならば,次のことが成り立ちます.
について微分可能なベクトル関数ならば,次のことが成り立ちます.
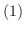 |
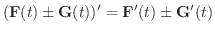 |
||
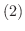 |
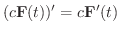 |
||
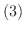 |
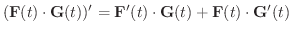 |
||
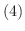 |
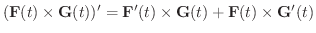 |
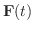 の大きさ
の大きさ
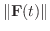 が定数のとき,
が定数のとき,
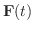 と
と
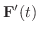 は全ての
は全ての  において直交することを示してみましょう.
において直交することを示してみましょう.
解
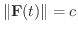 より,
より,
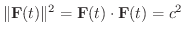 .
よってベクトル関数の微分法より
.
よってベクトル関数の微分法より
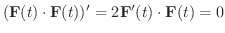
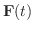 と
と
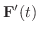 は直交します.
は直交します.

(a)
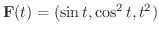 のとき,
のとき,
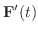 を求めよう.
を求めよう.
(b)
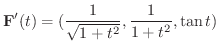 のとき,
のとき,
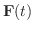 を求めよう.
を求めよう.
(c)
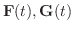 が
が  について微分可能なベクトル関数のとき,
について微分可能なベクトル関数のとき,
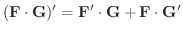
(d)
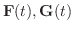 が
が  について微分可能なベクトル関数のとき,
について微分可能なベクトル関数のとき,