Next: 積分法(INTEGRATION) Up: 微分法(DIFFERENTIATION) Previous: 不定形の極限値(limit of indeterminate forms) 目次 索引
超越関数  を多項式を用いて表わすことができないでしょうか.もしそうなれば ,整関数さえ知っていれば他の関数のことを知らなくてすむのです.そんな疑問に イギリスの数学者 Brook Taylor (1685-1731) は1712年に答えてくれました.
を多項式を用いて表わすことができないでしょうか.もしそうなれば ,整関数さえ知っていれば他の関数のことを知らなくてすむのです.そんな疑問に イギリスの数学者 Brook Taylor (1685-1731) は1712年に答えてくれました.
 が点
が点 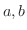 を含むある区間で
を含むある区間で 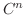 級であるならば,
級であるならば,
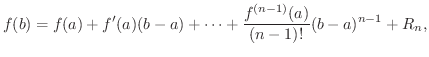
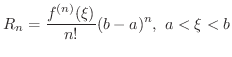
 が存在する.
が存在する.
証明
定数 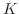 を
を
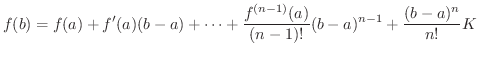
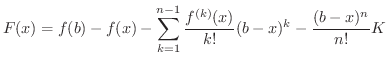
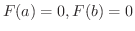 となり,
となり, 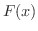 はRolleの定理の条件を満たす.したがって,Rolleの定理より
はRolleの定理の条件を満たす.したがって,Rolleの定理より
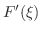 |
 |
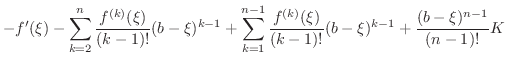 |
|
 |
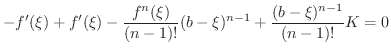 |
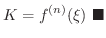
ここで用いられた 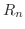 を Lagrangeの剰余数(Lagrange's remainder) といい,
を Lagrangeの剰余数(Lagrange's remainder) といい,
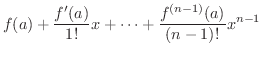
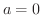 とおいて得られる定理を Maclaurinの定理 といい,
とおいて得られる定理を Maclaurinの定理 といい, 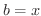 とおくと
とおくと
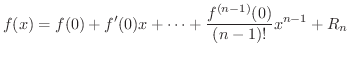
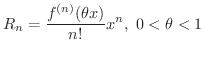
ここで誤差の評価は
![$\displaystyle \vert R_{n}\vert = \vert\frac{f^{(n)}(\theta x)}{n!}x^{n}\vert \l...
...max_{\theta \in [0,1]}\vert f^{(n)}(\theta x)\vert)\frac{\vert x\vert^{n}}{n!} $](img1792.png)
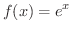 の Taylorの多項式とLagrangeの剰余数の誤差の評価を求めてみましょう.
の Taylorの多項式とLagrangeの剰余数の誤差の評価を求めてみましょう.
解
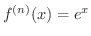 より
より
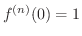 よって
よって
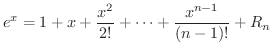
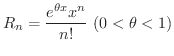 が成り立ちます.ところが,
が成り立ちます.ところが,
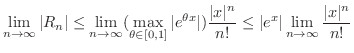
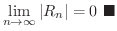
 は
は 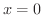 を含む区間
を含む区間 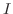 で
で
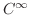 級関数とすると,Maclaurinの定理より任意の自然数
級関数とすると,Maclaurinの定理より任意の自然数  に対して,
に対して,
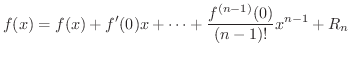
 であるならば
であるならば
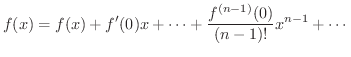
 の Maclaurin展開(Maclaurin expansion),または
の Maclaurin展開(Maclaurin expansion),または 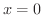 での Taylor展開(Taylor expansion) といいます.
での Taylor展開(Taylor expansion) といいます.
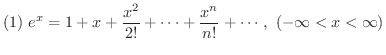
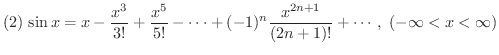
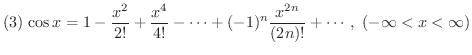
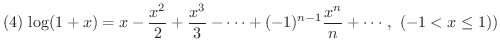
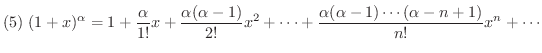
ただし,
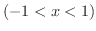
証明 (1)はすでに例題で行いました.
(2)
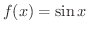 とすると
とすると
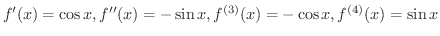 より
より
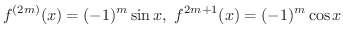
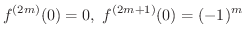
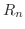 を計算すると
を計算すると
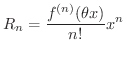
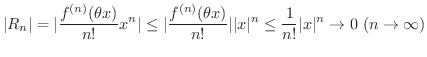
ここでE.G.H.Landau(1877-1938)によって用いられたちょっと便利な記号を紹介します.例えば関数 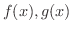 の間に
の間に
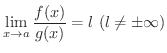
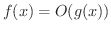
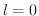 のとき,つまり
のとき,つまり
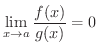
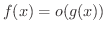
 が無限回微分可能だとし,
が無限回微分可能だとし, 次の多項式を作ってみます.すると,剰余項
次の多項式を作ってみます.すると,剰余項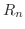 は
は
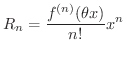
 が
が
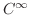 級より
級より
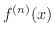 は連続となります.よって
は連続となります.よって
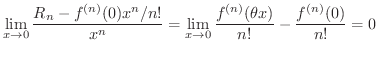
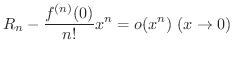
 が0を含むある区間で
が0を含むある区間で
 級ならば
級ならば
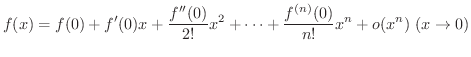
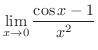
解
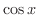 のMacLaurin展開より
のMacLaurin展開より
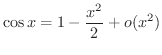 と表わせます.
よって
と表わせます.
よって
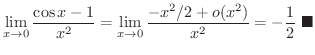
(c)
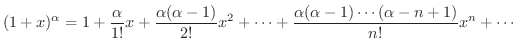
ただし,
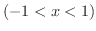
(d)
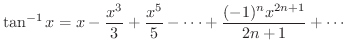 ,
,
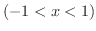
(a) 演習問題1(d)より,
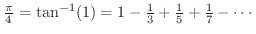 を得ることができる.これを用いて,プログラムを組み
を得ることができる.これを用いて,プログラムを組み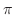 を小数点以下2桁まで求めてみよう.
を小数点以下2桁まで求めてみよう.
(b)
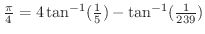 と表した式をMachinの公式という.この公式を用いて
と表した式をMachinの公式という.この公式を用いて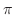 を小数点以下100桁まで求めてみよう.
を小数点以下100桁まで求めてみよう.