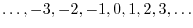...\space 0.1
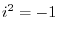${\mathbb R}$ or the interval $(-\infty,\infty)$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... contrapositive.1.1
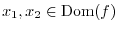A statement is an assertion that can be determined to be true or false. We use $p,q$ for statements. The statement 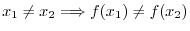$p \longrightarrow q$ becomes false only if 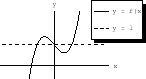$p$ is true and 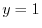$q$ is false. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...#tex2html_wrap_inline37628#1.2
How to find the inverse
1. Replace 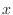$x$ by $y$.
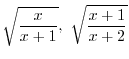2. Solve for $y$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 1rad1.3
radian. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.... 1.4
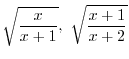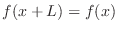When the function satisfies $f(x + L) = f(x)$, we say 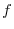$f(x)$ has the period $L$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... induction.1.5
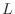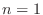Show the statement is true for $n=1$ and assume true 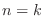$n=k$. If the statement is true for 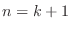$n=k+1$, then it is ture for all $n$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...\space 1.6

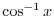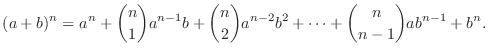
$\displaystyle (a + b)^n = a^n + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b^2 + \cdots + \binom{n}{n-1}ab^{n-1} + b^{n}. $

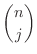is called binomial theorem and $\displaystyle{\binom{n}{j}}$ is called binomial coefficient. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... class="CENTER"17181>% latex2html id marker 41003 \includegraphics[width=3.5cm]{SOFTFIG-1/logteigiiki_gr1.eps}1.7
A logarithmic function can not take the values less than 0. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.... 2.1
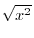To be differentiable, the limit $A$ must be real number. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... \\2.2
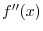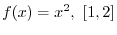The neighborhood of $x = a$ is the interval $(a-\delta, a + \delta)$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.