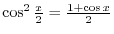Next: Graph of Trig Functions Up: Functions Previous: Functions of single variable Contents Index
| Radians |
|---|
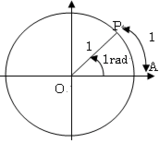
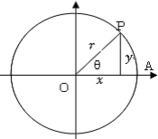
As in the figure, we let the origin O. Take points
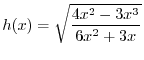 on the unit circle on the unit circle
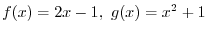 . Now set . Now set
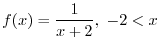 as as 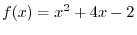 . The angle . The angle
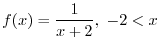 for which the arclength of AP is 1 is called 1 radian and denoted by 1rad1.3. for which the arclength of AP is 1 is called 1 radian and denoted by 1rad1.3.
|
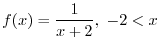 is
is 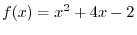 degree and
degree and  radian. Then
radian. Then
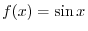
| Degree | 0 | 30 | 45 | 60 | 90 | 120 | 150 | 180 | 360 |
| Radian | 0 |
 |
 |
 |
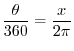 |
 |
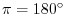 |
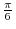 |
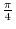 |
NOTE As Trigonometric Functions
Suppose that
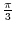 . Then the following functions of
. Then the following functions of 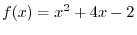 are called Trigonometric functions.
are called Trigonometric functions.
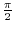
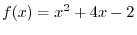 chages the value, the point P
chages the value, the point P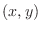 and the shape of the right triangle
and the shape of the right triangle 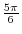 OPH changes.
OPH changes.
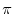 2.
2.
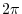 3.
3.
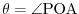 4.
4.
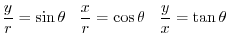
SOLUTION 1. Draw a unit circle with the origin O and draw a line OP with
 . Then the value of
. Then the value of  coordinate of P is equal to
coordinate of P is equal to
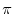 .
.
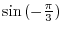
 coordinate of P where
coordinate of P where
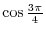 is equal to
is equal to
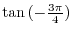 . Thus we have
. Thus we have
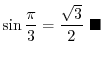
3. The value of  coordinate of P where
coordinate of P where
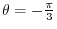 is equal to
is equal to
 . Thus we have
. Thus we have
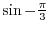
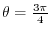 so that
so that  coordinate is -1. Then the ratio of the values of
coordinate is -1. Then the ratio of the values of  coordinate and
coordinate and  coordinate is
coordinate is
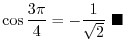 . Thus we have
. Thus we have
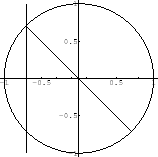
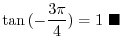 2.
2.
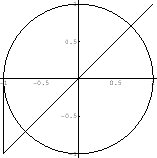 3.
3.
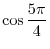
SOLUTION 1. Draw a unit circle with the origin O and draw a line OP with
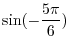 . Then the value of
. Then the value of  coordinate of P is equal to
coordinate of P is equal to
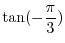 . Thus we have
. Thus we have
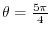
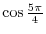 . Then the value of
. Then the value of  coordinate of P is equal to
coordinate of P is equal to
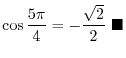 . Thus we have
. Thus we have
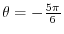
3. Stretch the line OP with
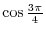 so that
so that  coordinate is 1. Then the ratio of the values of
coordinate is 1. Then the ratio of the values of  coordinate and
coordinate and  coordinate is
coordinate is
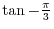 . Thus we have
. Thus we have
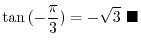
NOTE 1. Consider the point PBasic Trig Identities
For all
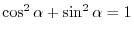 ,
,
1.
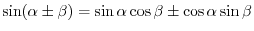
2.
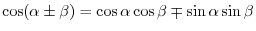
3.
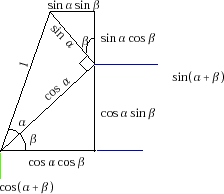
 on the unit circle. Then
on the unit circle. Then
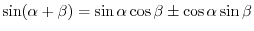
2. ,3. Look at the figure, you will see
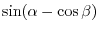
2. ,3. Write
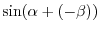 as
as
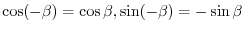 and note that
and note that
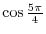 .
.
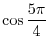 .
.
SOLUTION
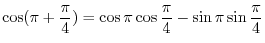 |
 |
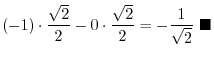 |
|
 |
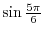 |
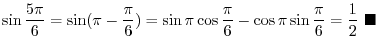 .
.SOLUTION
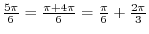
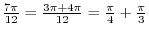 .
.
SOLUTION
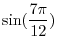 . Now using trigonometric addition formula, we have
. Now using trigonometric addition formula, we have
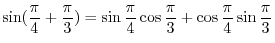 |
 |
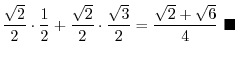 |
|
 |
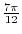 |
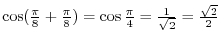 .
.
SOLUTION
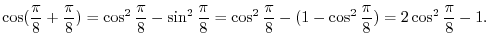 . Using trigonometric addition formula�
. Using trigonometric addition formula�
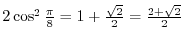
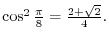 .
.
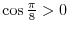 Here,
Here,
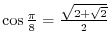 , we have
, we have