Next: Inverse Trigonometric Functions Up: Trigonometric Function Previous: Trigonometric Function Contents Index
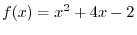 to express the angle. But from now on, we use
to express the angle. But from now on, we use  as independent variable and
as independent variable and  as dependent variable. In other words, we write
as dependent variable. In other words, we write
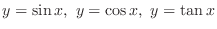
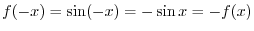 . Since
. Since
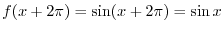 ,
,
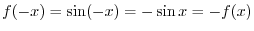 is an odd function and symmetric with respect the origin.
Also, the function satisfies
is an odd function and symmetric with respect the origin.
Also, the function satisfies
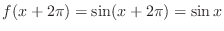 . Thus
. Thus
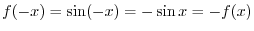 has the period
has the period 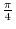 . 1.4 From these information, we can draw the graph of
. 1.4 From these information, we can draw the graph of
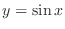 by checking the values of
by checking the values of  from 0 to
from 0 to 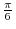 and corresponding values of
and corresponding values of  .
.
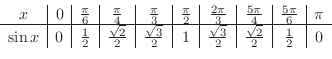
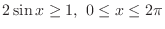
SOLUTION Since
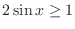 , we have
, we have
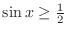 . The region satisfying
. The region satisfying
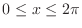 and
and
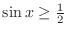 is the set of points
is the set of points 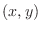 such that
such that
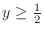 .
Thus,
.
Thus,
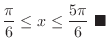
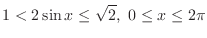
SOLUTION We separate
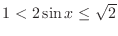 into two inequalities such as
into two inequalities such as
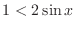 and
and
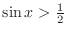 . The region satisfying
. The region satisfying
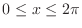 and
and
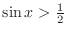 is the set of points
is the set of points 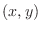 such that
such that
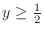 .
Now
.
Now
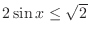 implies that
implies that
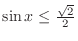 . Thus the region satisfying
. Thus the region satisfying
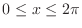 and
and
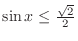 is the set of all points
is the set of all points 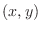 such that
such that
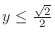 .
See the figure.
Putting these toghether, we have
.
See the figure.
Putting these toghether, we have
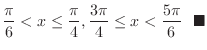
Next we probe the graph of the function
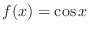 . Since
. Since
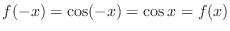 ,
,
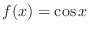 is an even function and symmetric with respect to the
is an even function and symmetric with respect to the  -axis. Furthermore,
-axis. Furthermore, 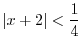 satisfies
satisfies
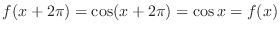 . Thus,
. Thus,  has the period
has the period 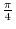 .
.
Thus to draw the graph of
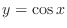 , it is enough to check the values of
, it is enough to check the values of  from 0 to
from 0 to 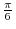 . From these information, we can draw the graph of
. From these information, we can draw the graph of
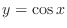 by checking the values of
by checking the values of  from 0 to
from 0 to 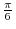 and corresponding values of
and corresponding values of  .
.
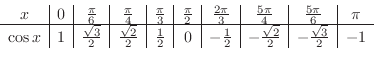
Now note that the functions
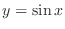 and
and
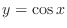 satisfy the relation
satisfy the relation
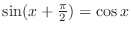 .
.
![\includegraphics[width=7cm]{SOFTFIG-1/Fig1-2-0-1_gr1.eps}](img438.png)
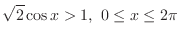
SOLUTION Since
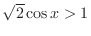 , we have
, we have
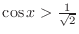 . The region satisfying
. The region satisfying
 and
and
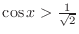 is the set of points
is the set of points 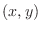 so that the value of
so that the value of
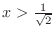 .
From the figure, we have
.
From the figure, we have
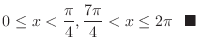
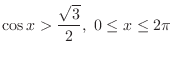
SOLUTION The region satisfying
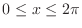 and
and
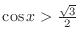 is the set of points
is the set of points 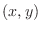 such that the value of
such that the value of
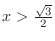 .
.
From this figure, we have
At the end we investigate the graph of function
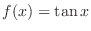 . Since
. Since
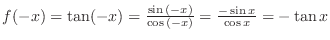 ,
,
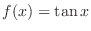 must be symmetric with respect to the origin. Furthermore, the function satisfies the following:
must be symmetric with respect to the origin. Furthermore, the function satisfies the following:
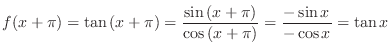
 is a periodic function with the period
is a periodic function with the period 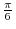 . This means that to draw the graph of the function
. This means that to draw the graph of the function
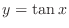 , it is enough to check the values of
, it is enough to check the values of  such that
such that
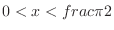 and corresponding
and corresponding  . We note that the function
. We note that the function 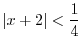 is not defined at
is not defined at
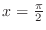 . To overcome this problem, we use the limit:
. To overcome this problem, we use the limit:
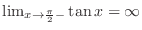 .
.
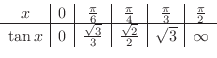
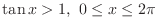
SOLUTION The region satisfying
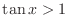 is the set of points
is the set of points 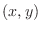 such that either
such that either 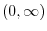 and
and 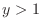 or
or 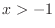 and
and 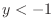 .
From the figure, we have
.
From the figure, we have
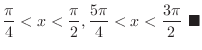
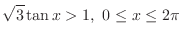
SOLUTION The region satisfying
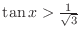 is the set of points such that either
is the set of points such that either 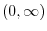 and
and
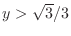 or
or 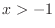 and
and
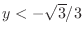 .
Thus, we have
.
Thus, we have
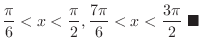
|
Exercise A
|
 -axis?Dprovided
-axis?Dprovided
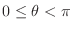 ?D
?D
![[*]](crossref.png) , Solve the following inequalities, provide
, Solve the following inequalities, provide
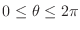 ?D
?D
|
Exercise B
|
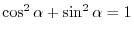 ?Cshow the following identities hold?D
?Cshow the following identities hold?D
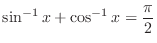 is true for all
is true for all  ?D
?D