Next: Limit of Sequence Up: Functions Previous: Graph of Trig Functions Contents Index
NOTE The domain of
Arcsin 
Let
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img504.png) be the domain of the function
be the domain of the function
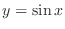 . Then the function
. Then the function
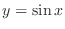 becomes one-to-one. Thus we can think of the inverse function. We write this function as
becomes one-to-one. Thus we can think of the inverse function. We write this function as
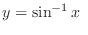 or
or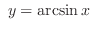
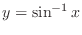 is the range of
is the range of
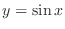 . Thus we have
. Thus we have ![$[-1,1]$](img509.png) . On the other hand, the range of
. On the other hand, the range of
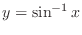 is the domain of
is the domain of
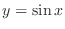 . Thus we have
. Thus we have
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img504.png) .
In other words,
.
In other words,
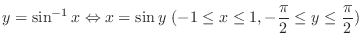
![$[-\frac{\pi}{2},\frac{\pi}{2}]$](img511.png) is called principal value of arcsin
is called principal value of arcsin  .
.
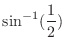
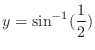 means
means
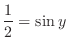 . Note also the values of
. Note also the values of  must be in the interval
must be in the interval
![$\displaystyle{[\frac{-\pi}{2}, \frac{\pi}{2}]}$](img519.png) .
Since
.
Since 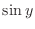 takes the value
takes the value
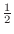 for
for
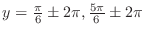 ,
,  must be in
must be in
![$\displaystyle{[\frac{-\pi}{2}, \frac{\pi}{2}]}$](img519.png) . Thus we have
. Thus we have
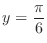

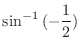 .
.
SOLUTION
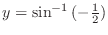 is equivalent to
is equivalent to
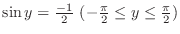 . Thus,
. Thus,
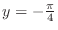

NOTE The domain of the function
Arccos 
Let the interval ![$[0,\pi]$](img527.png) be the domain of
be the domain of
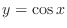 . Then
. Then
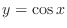 becomes one-to-one. Thus we can think of the inverse function. We write this function as
becomes one-to-one. Thus we can think of the inverse function. We write this function as
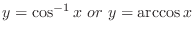
 .
.
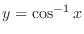 is
is ![$[-1,1]$](img509.png) which is the range of the function
which is the range of the function
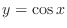 . The range of the function
. The range of the function
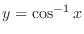 is
is ![$[0,\pi]$](img527.png) .
Thus
.
Thus
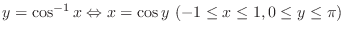
![$[0,\pi]$](img527.png) is called pv of arccos
is called pv of arccos .
.
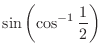 .
. 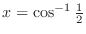 is equivalent to
is equivalent to
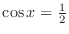 for
for
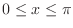 , we have
, we have
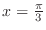 . Thus
. Thus
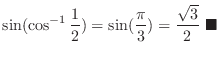
 which satisafies
which satisafies
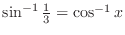 .
. 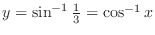 . Then
. Then
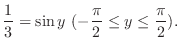
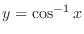 , we have
, we have
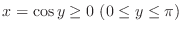 . Note that,
. Note that,
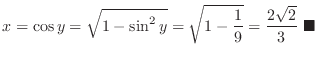
| ArcTan |
|---|
Let the interval
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img504.png) be the domain of the function be the domain of the function
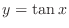 . Then the function . Then the function
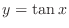 becomes one-to-one. Thus we can think of the inverse function. We write this function as becomes one-to-one. Thus we can think of the inverse function. We write this function as
 or or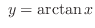
 . .
|
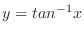 is the range of the function
is the range of the function
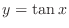 which is
which is
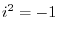 . The range is
. The range is
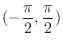 . Thus we have
. Thus we have
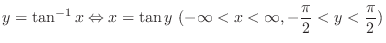
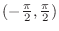 is called principal value of arctan
is called principal value of arctan .
.
 satisfies the following.
satisfies the following.
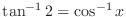 2.
2.
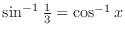
SOLUTION 1. Set
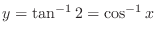 . Then
. Then
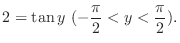
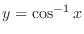 , we have
, we have
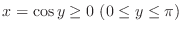 . Now dividing both sides of the identity
. Now dividing both sides of the identity
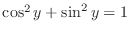 by
by
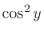 and noting
and noting
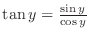 , we have
, we have
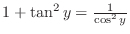 . Thus,
. Thus,
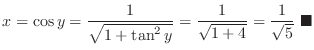
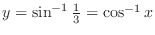 . Then
. Then
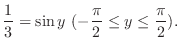
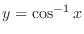 , we have
, we have
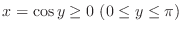 . Substitute this into the identity
. Substitute this into the identity
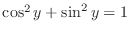 , we have
, we have
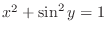 . Thus,
. Thus,
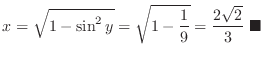
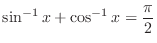 holds for all
holds for all  .
. 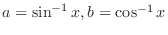 . Then we have
. Then we have
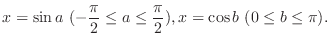
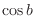 as
as
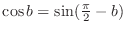 . Then
. Then
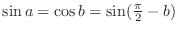 .
Since
.
Since
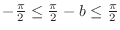 , the function
, the function 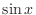 is one-to-one. Thus
is one-to-one. Thus
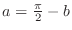 . Since
. Since
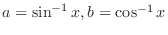 , we obtain
, we obtain
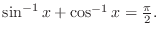

|
Exercise A
|
|
Exercise B
|
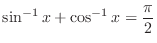 is true for all
is true for all  ?D
?D