Next: Limit of Functions Up: Functions Previous: Inverse Trigonometric Functions Contents Index
| Sequences |
|---|
For each number of
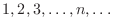 , there corresponds unique real number , there corresponds unique real number
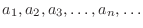
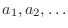 term. term.
|
 th term is found, all terms can be derived. Thus we call the
th term is found, all terms can be derived. Thus we call the  th term general term.
th term general term.
| Bounded sequence |
|---|
A sequence  is called bounded above if there exists a number is called bounded above if there exists a number 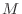 such that such that
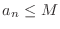 for all for all  . A sequence . A sequence  is called bounded below if there exists a number is called bounded below if there exists a number 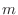 such that such that
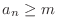 for all for all  . Furthermore, a sequence . Furthermore, a sequence  is called bounded if it is bounded above and bounded below.. is called bounded if it is bounded above and bounded below..
|
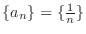 is bounded. For
is bounded. For
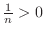 and
and
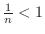 for all
for all  .
.
Monotonicity If
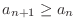 for all
for all  , a sequence
, a sequence  is called monotonically increasing. If
is called monotonically increasing. If
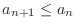 for all
for all  , a sequence
, a sequence  is called monotonicall decreasing sequence.
is called monotonicall decreasing sequence.
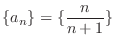 is monotonically increasings.
is monotonically increasings.
SOLUTION We use the ratio to check to see. Note that
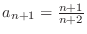 .
.
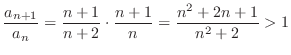
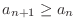 and
and  is monotonically increasing
is monotonically increasing

SOLUTION Since
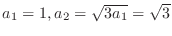 , we have
, we have
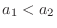 . Now use mathematical induction. 1.5
. Now use mathematical induction. 1.5
For 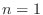 ,
,
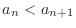 is true. Now assume that
is true. Now assume that
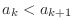 is true. Then we have
is true. Then we have
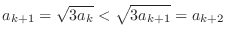
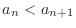 for all
for all 

NOTE When a sequence converges to Limit of sequence As  approaches
approaches 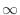 ,
, 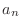 approaches
approaches 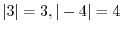 . Then we write
. Then we write
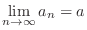
 converges to
converges to 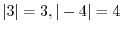 and call this
and call this 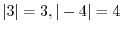 limit.
limit.
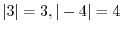 ,
, 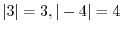 has to be a real number. Thus we can not use
has to be a real number. Thus we can not use 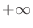 or
or 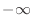 for
for 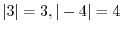 . When a sequence
. When a sequence  does not converge, we say
does not converge, we say  diverges.
diverges.
NOTE When the limit exits, four arithmetic operations hold. Express 1. by
Limit properties
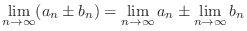
NOTE Suppose that the denominator of the sequence approaches some positive constant as the numerator approaches Limit properties
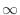 , Then the sequence gets larger without bound. Thus the sequence diverges. Suppose next that the denominator of the sequence approaches
, Then the sequence gets larger without bound. Thus the sequence diverges. Suppose next that the denominator of the sequence approaches 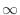 as the numerator approaches a positive constant. Then the limit of the sequence is 0.
as the numerator approaches a positive constant. Then the limit of the sequence is 0.
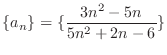
SOLUTION
As
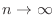 ,
,
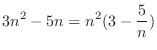
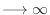 and
and
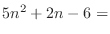
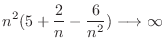 . Then we factor by taking out
. Then we factor by taking out 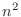 to have
to have
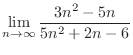 |
 |
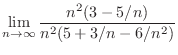 |
|
 |
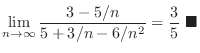 |
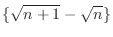
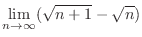 |
 |
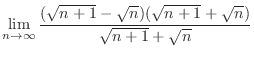 |
|
 |
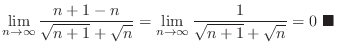 |
To find the limit, the theorem above is not enough. For example, consider
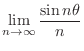 as
as
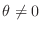 .
In this problem, we can not obtain the limit by using the theorem 1.1 and the theorem 1.2. To find the limit of
.
In this problem, we can not obtain the limit by using the theorem 1.1 and the theorem 1.2. To find the limit of
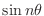 , it is useful to use the following theorem.
, it is useful to use the following theorem.
| Squeezing theorem |
|---|
|
Theorem 1..3 If there exists a number
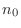 so that so that
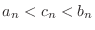 is true for all is true for all 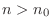 and and
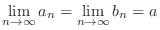
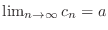 . . |
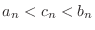 , we have either
, we have either
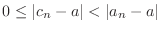 or
or
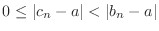 .
Note that
.
Note that
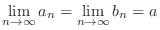
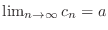

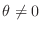 , find the limit of the following.
, find the limit of the following.
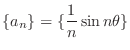
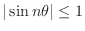 , we have
, we have
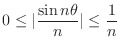
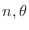 . Thus we can sandwich
. Thus we can sandwich
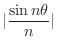 using 0 and
using 0 and
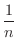 . Now taking the limit of 0 and
. Now taking the limit of 0 and
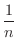 , we obtain
, we obtain
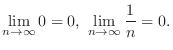
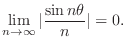
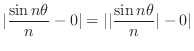
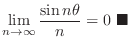
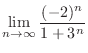 2.
2.
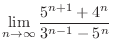
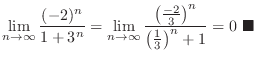 2.
2.
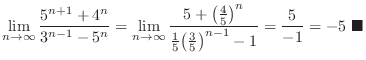
The limit of 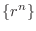 is a base of convergence and divergence.
is a base of convergence and divergence.
Proof
Bernoulli inequality
For 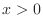 and
and 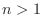 ,
,
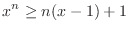
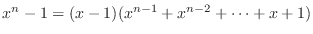 .
.
For 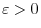 , we have
, we have 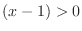 and
and
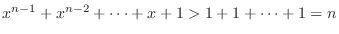
For 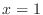 , we have
, we have 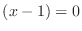 and
and
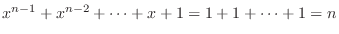
For 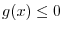 , we have
, we have 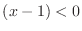 and
and
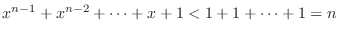 . Thus,
. Thus,
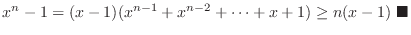
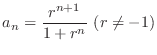 , find
, find
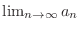 .
. 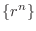 .
.
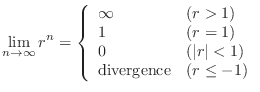
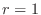 ,
,
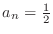 and
and
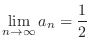 .
For
.
For 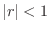 ,
,
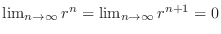 and
and
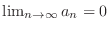 .
.
For
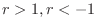 ,
,
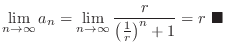
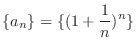 is monotonically increasing.
is monotonically increasing. 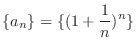 , we have
, we have
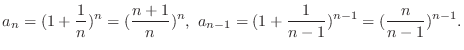
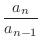 |
 |
![$\displaystyle (\frac{n+1}{n})^{n}(\frac{n-1}{n})^{n-1} = \frac{n}{n-1}[(\frac{n+1}{n})(\frac{n-1}{n})]^n$](img719.png) |
|
 |
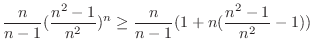 |
||
 |
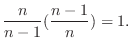 |
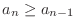 and
and  is monotonically increasing
is monotonically increasing

| Monotone convergence theorem |
|---|
|
Theorem 1..4 Every increasing sequence that is bounded above converges. Every decreasing sequence that is bounded below converges..
|
 is monotonically increasing and bounded above, then there exists a number for which the sequence
is monotonically increasing and bounded above, then there exists a number for which the sequence  can not become greater than that number. Among all those numbers, we let the least number be
can not become greater than that number. Among all those numbers, we let the least number be 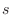 . Then the difference between
. Then the difference between 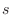 and
and 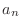 becomes small. Thus the sequence
becomes small. Thus the sequence  converges.
converges.
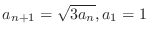 . Determine the sequence
. Determine the sequence  converges or diverges..
converges or diverges..  converges.
By Exercise1.14, we know
converges.
By Exercise1.14, we know  is monotonically increasing sequence. So, we need to show the sequence is bounded above. We use mathematical induction on
is monotonically increasing sequence. So, we need to show the sequence is bounded above. We use mathematical induction on  .
.
Since
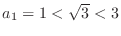 , it is true for
, it is true for 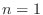 .
.
Assume that 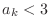 . Then
. Then
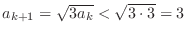 . Thus for all
. Thus for all  ,
, 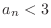 and
and  is bounded above increasing sequence. Therefore,
is bounded above increasing sequence. Therefore,  converges
converges

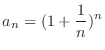 . Determine the sequence
. Determine the sequence  converges or diverges.
converges or diverges. 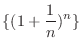 is monotonically increasing. Thus we need to show the sequence is bounded above.
is monotonically increasing. Thus we need to show the sequence is bounded above.
Expand
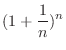 1.6using binomial theorem,
1.6using binomial theorem,
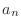 |
 |
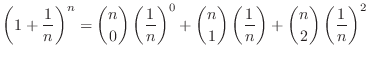 |
|
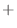 |
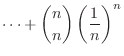 |
||
 |
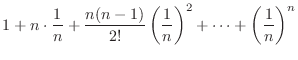 |
||
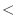 |
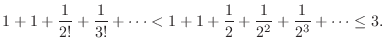 |
 is bounded above increasing sequnce and converges
is bounded above increasing sequnce and converges

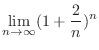
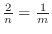 . Then
. Then
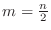 and
and
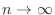 implies that
implies that
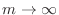 . Thus,
. Thus,
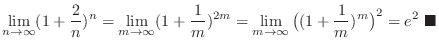
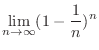
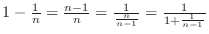 , we have
, we have
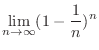 |
 |
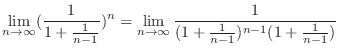 |
|
 |
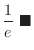 |
NOTE Since
Limit ratio test
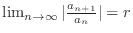 , for all
, for all  such that
such that 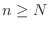 , we have
, we have
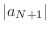
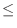
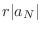
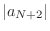
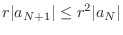
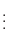
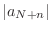
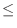
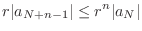
Noting that
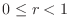 , we have
, we have
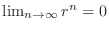 . Thus,
. Thus,
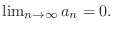
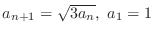
SOLUTION
Note that if  converges to
converges to 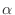 , then
, then
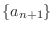 converges to
converges to 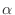 . Thus we have
. Thus we have
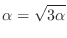
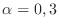 . Since
. Since 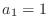 , it is impossible to have
, it is impossible to have
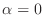 . So we have
. So we have
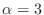 . Note this is not the end of proof. We have to show
. Note this is not the end of proof. We have to show
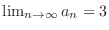 .
By the limit ratio test, it is enough to show
.
By the limit ratio test, it is enough to show
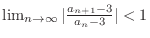 .
.
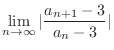 |
 |
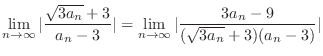 |
|
 |
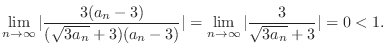 |
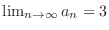

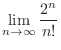
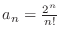 . Then
. Then
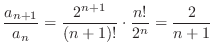
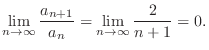
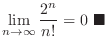
|
Exercise A
|
 of the following sequences:
of the following sequences:
|
Exercise B
|
![$\displaystyle{\lim_{n \rightarrow \infty}\sqrt[n]{a} = 1}$](img825.png) for
for 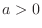 ?D
?D
![$\displaystyle{\lim_{n \rightarrow \infty}\sqrt[n]{a} = 1}$](img825.png) , find the limit of the followings:
, find the limit of the followings:
 ?D
?D