Next: Differentiation Up: Functions Previous: Properties of Continuous Functions Contents Index
| Definition of Exponents |
|---|
Let 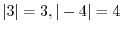 be a positive real number, be a positive real number,  be a natural number, be a natural number, 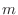 be an integer. Then be an integer. Then
|
NOTE At 5. Consider the case 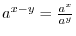 and
and
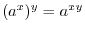 . First we create an increasing sequence of rational numbers which converges to
. First we create an increasing sequence of rational numbers which converges to 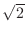 , say
, say
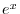 . For example,
. For example,
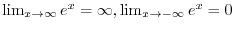
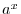 , we have
, we have
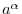 and
and
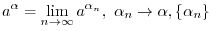
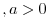 is increasing . Also
is increasing . Also
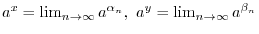 implies that
implies that
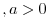 is a bounded above increasing sequence. Thus it converges.
Let
is a bounded above increasing sequence. Thus it converges.
Let
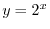
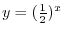 . The proof looks OK. But there are many rational valued sequences which converge to
. The proof looks OK. But there are many rational valued sequences which converge to 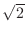 . So, we have to show using other rational sequence
. So, we have to show using other rational sequence 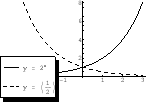 which converges to
which converges to 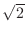 ,
,
 is the same. In mathematics, we call this Uniqueness.
is the same. In mathematics, we call this Uniqueness.
Let
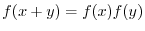 be two increasing rational valued sequences which converege to
be two increasing rational valued sequences which converege to 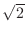 . Since
. Since
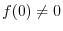 , for all
, for all  satisfying
satisfying
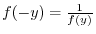 , we can choose
, we can choose
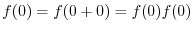 so that
so that
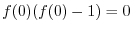 .
For
.
For 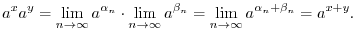 ,
,
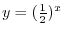 ,
,
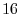
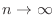 implies that
implies that
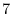 and by the squeezing theorem,
and by the squeezing theorem,
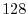
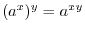 is independent from the choice of
is independent from the choice of  .
.
For 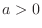 and
and 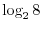 , a function
, a function 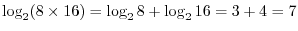 is called Exponential Function .
is called Exponential Function .
The domain is
 and the range is
and the range is
 .
.
Laws of Exponential Function
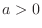 . Then for every real numbers
. Then for every real numbers  , we have
, we have
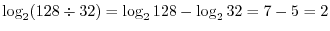
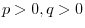
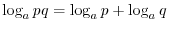
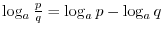
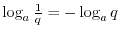 is continuous on
is continuous on
 and strictly increasing function.
and strictly increasing function.
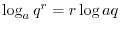
NOTE 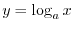 for
for 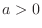 is defined for irrational number
is defined for irrational number  by considering
by considering
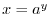 .
.
 sequence of rational numbers
sequence of rational numbers 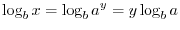
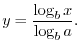 and
and
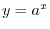
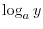 and
and
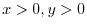 .
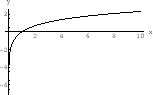
. and corresponding values of
and corresponding values of  . Then plot those points and connect by smooth curve.
. Then plot those points and connect by smooth curve.
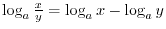
 satisfies
satisfies
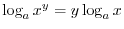 for all
for all  and
and
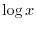 . Show the followings.
. Show the followings.
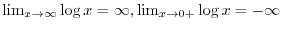 2.
2.
SOLUTION 1. We can write
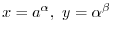 . Then
. Then
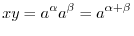 . Since
. Since
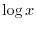 , we have
, we have 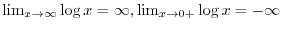

2.
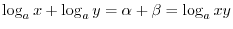 implies that
implies that


NOTE Definition of Logarithm Let  be a positive real number and
be a positive real number and 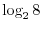 . The for every real number
. The for every real number  and
and 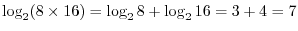 , we write
, we write
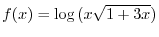 and call
and call  base of Logarithm.
base of Logarithm.
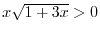 . Find the number above
. Find the number above  and the number above
and the number above 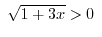 . Then we have 3 and 4. Now add these two numbers to obtain
. Then we have 3 and 4. Now add these two numbers to obtain 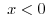 . Then the numer below
. Then the numer below 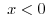 is
is 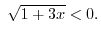 the result of
the result of
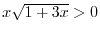 . Express the number 3 above 8 as
. Express the number 3 above 8 as
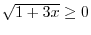 . Then we get
. Then we get
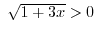 . Next we calclulate
. Next we calclulate
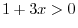 . This time we subtract the number above 128 from the number above 32. Then we get
. This time we subtract the number above 128 from the number above 32. Then we get 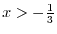 . Now the number 4 is the result of
. Now the number 4 is the result of
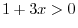 . Thus
. Thus
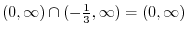 .
.
Laws of Logarithmics
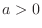 ,
, 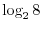 ,
,
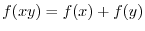 . Then we have the followings.
. Then we have the followings.
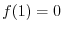
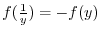
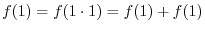
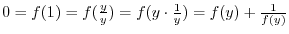
NOTE
Consider
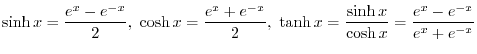 . Then by the definition of logarithm, we have
. Then by the definition of logarithm, we have 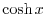 . Now take the logarithm of both sides with the base
. Now take the logarithm of both sides with the base 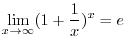 . Then
. Then
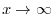
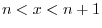
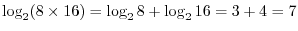 is
is
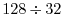 , and
, and 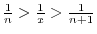 is strictly increasing and continuous function. Thus there exists a unique inverse function and we write
is strictly increasing and continuous function. Thus there exists a unique inverse function and we write
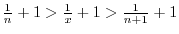 . Note
. Note
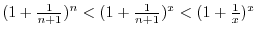 is defined and continuous on
is defined and continuous on
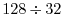 . we say
. we say
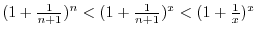 logarithmic function with base
logarithmic function with base 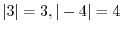 .
.
Laws of Logarithmic Functions
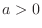 . Then for every real numer
. Then for every real numer
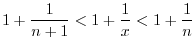 , we have the followings.
, we have the followings.
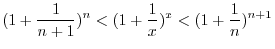
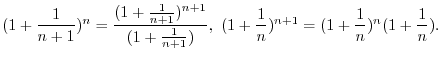
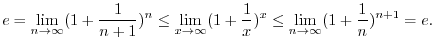
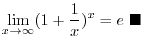
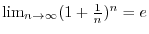 is continuous and monotonically increasing on
is continuous and monotonically increasing on
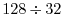
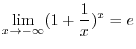
NOTE
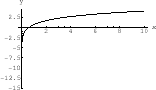
To show 2. Let
 . Then
. Then
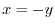 and
and
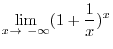

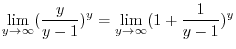
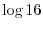 . Thus,
. Thus,
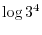 and
and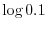 or
or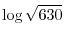 and
and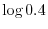
 implies
implies
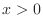 and
and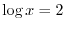 . Since a square root function can not take negative values, we have
. Since a square root function can not take negative values, we have
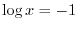 . Thus
. Thus 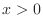 and
and
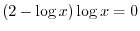 . Express using interval, we have
. Express using interval, we have
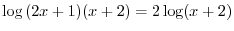

 satisfies
satisfies
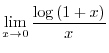 for
for
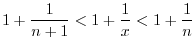 . Then
. Then
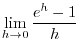 2.
2.
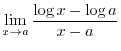
SOLUTION 1.
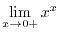 implies
implies 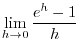

2.
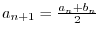 implies that
implies that
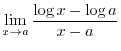

Hyperbolic Functions
A function below is called hyperbolic function.
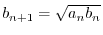
 is used.
is used.
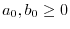 .
.
SOLUTION
As
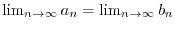 , there exists
, there exists  which satisfies
which satisfies
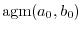 . Thus
. Thus
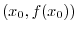
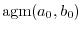 one more time to get
one more time to get
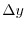
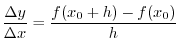 .
. 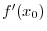 . Then
. Then
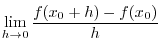 |
 |
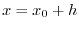 |
|
 |
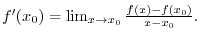 |
||
 |
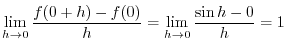 |
|
Exercise A
|
|
|
Exercise B
|
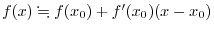 and the geometric mean
and the geometric mean
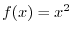 . Answer the following questions:
. Answer the following questions:
(a) Show  and
and 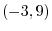 converge for
converge for
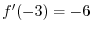 .
.
(b) Show
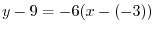 . This limit is denoted by
. This limit is denoted by
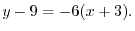 ?D
?D