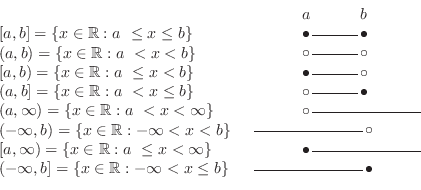Next: Inequalities Up: Introduction Previous: Introduction Contents Index
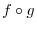 . Integers are the natural numbers with 0 and negative numbers such as
. Integers are the natural numbers with 0 and negative numbers such as
 . Rational numbers are fractions of integers
. Rational numbers are fractions of integers
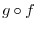 with non-zero denominator
with non-zero denominator  . Irrational number are numbers with non repeated infinite decimals such as
. Irrational number are numbers with non repeated infinite decimals such as
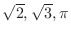 . Real numbers are either rational numbers or irrational numbers. Furthermore,
. Real numbers are either rational numbers or irrational numbers. Furthermore, 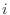 satisfying
satisfying 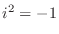 is called the imaginary unit.
The set of real numbers can be expressed either using the symbol
is called the imaginary unit.
The set of real numbers can be expressed either using the symbol
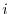 0.1The real numbers can be thought of as points on a number line. In other words, every real number can be put into one-on-one correspondence with the point on the number line.
0.1The real numbers can be thought of as points on a number line. In other words, every real number can be put into one-on-one correspondence with the point on the number line.
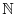
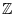 , we define
, we define
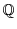
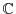 absolute value of
absolute value of  .
For example,
.
For example,
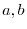 . Now carefully look at
. Now carefully look at
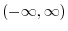 . For if
. For if 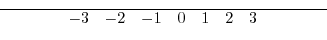 , then we have
, then we have
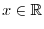 . For if
. For if 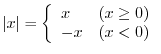 , then we have
, then we have
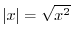 . This means that
. This means that
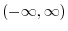 and
and 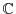 give rise the same number. Thus, we can say
give rise the same number. Thus, we can say
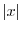 .
For example,
.
For example,
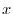 .
.
| Element of the set |
|---|
A distinct object 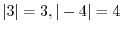 belongs to the set belongs to the set 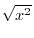 is called the element of the set is called the element of the set 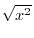 and denoted by and denoted by 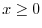 . .
|
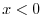 . Then we write
. Then we write
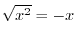 and say 3 is an element of
and say 3 is an element of
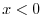 . 0 is not a natural number. Then we write
. 0 is not a natural number. Then we write
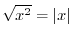 .
.
| Subset |
|---|
If all elements of 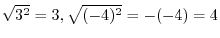 are also elments of are also elments of 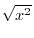 , then , then 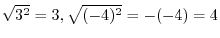 is subset of is subset of 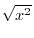 and denoted by and denoted by
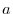 . .
|
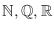 , we must have
, we must have
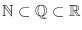 .
.
| Union |
|---|
The Union of tow sets 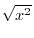 and and 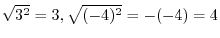 is the collection of points which are in is the collection of points which are in 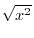 or in or in 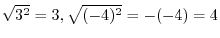 or in or in 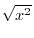 and and 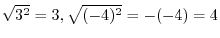 , and denoted by , and denoted by 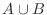 . .
|
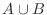 consists of all elements of
consists of all elements of 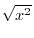 and elements of
and elements of 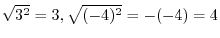 .
.
| Intersection |
|---|
The Intersection of two sets 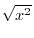 and and 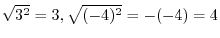 is the collection of points which are in is the collection of points which are in 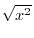 and and 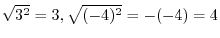 and denoted by and denoted by 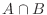 . .
|
NOTE The set 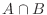 consists of elements which have both properties of
consists of elements which have both properties of 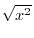 and
and 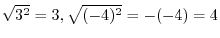 .
.
Subsets of